設計師在設計的時候，總會遇到這樣那樣的問題，和人PK不斷，修改不斷。界面區域多大合適呢？ICON多大？顏色區間多少？為什麼這麼定義？什麼是普世的美？很多UIer都說，50%靠設計，50%靠交流，那麼在交流的時候如何說服別人呢？ADS定位、用戶群、用戶環境、調研都可以作為參考的依據，在這裡再向大家介紹一下我們身邊存在的黃金分割，希望作為設計的利器，或創作或PK。
一.植物
“黃金角度”生物學家發現植物種類繁多、葉子形態各異，但是葉子在莖上的排列卻有著特殊的規律.我們從某種植物的頂端往下看，便會發現上下層相鄰的兩片葉子之間所構成的角約為137.50,如果每層葉子只畫一片來表示，第一層和第二層的相鄰兩葉之間的角度約為137.50,以後二層到三層、三層到四層、四層到五層……兩葉之間都成這個角度，這個角度對葉子的通風和采光最為有利.這葉子之間的137.50角與黃金數又有什麼聯系呢？我們知道，一周為3600，137.50： =137.50：222.50≈0.618.也就是說，各種植物葉子的生長規律中自然隱藏著黃金數。
向日葵花有89個花辮，55個朝一方，34個朝向另一方
楓葉
噴嚏麥
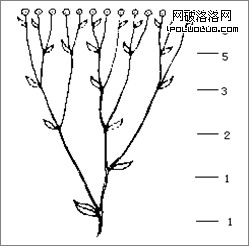
1.1.2.3.5.8.13.21.34.55.89.144…
後面的數除以前面的樹，越往後越趨向於黃金比例。運用到設計當中，譬如一個齒輪的圖標，齒的個數可以參考這組數列。PK詞：這是自然的法則。
二.動物
由這組數列引出斐波那契曲線，斐波納契是在解一道關於兔子繁殖的問題時，得出了這個數列。假定你有一雄一雌一對剛出生的兔子，它們在長到一個月大小時開始交配，在第二月結束時，雌兔子產下另一對兔子，過了一個月後它們也開始繁殖，如此這般持續下去。每只雌兔在開始繁殖時每月都產下一對兔子，假定沒有兔子死亡，在一年後總共會有多少對兔子？ • 在一月底，最初的一對兔子交配，但是還只有1對兔子；在二月底，雌兔產下一對兔子，共有2對兔子；在三月底，最老的雌兔產下第二對兔子，共有3對兔子；在四月底，最老的雌兔產下第三對兔子，兩個月前生的雌兔產下一對兔子，共有5對兔子；……如此這般計算下去，兔子對數分別是：1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, …看出規律了嗎？ •從第3個數目開始，每個數目都是前面兩個數目之和。
下面再簡單介紹下斐波那契，了解下周邊總是可以唬人的。
意大利數學家，12、13世紀歐洲數學界的代表人物。生於比薩，早年跟隨經商的父親到北非的布日伊（今阿爾及利亞東部的小港口貝賈亞），在那裡受教育。以後到埃及、敘利亞、希臘、西西裡、法國等地游歷，熟習了不同國度在商業上的算術體系，他認為使用印度－阿拉伯數碼最方便。1200年左右回到比薩，潛心寫作。 他的書保存下來的共有5種。最重要的是《算盤書》（1202年完成，1228年修訂），算盤並不單指羅馬算盤或沙盤，實際是指一般的計算。全書共15章，1～7章系統介紹了印度數碼與記數制度，以及整數、分數的各種計算方法，結果用棄九法來驗算。還列有乘法表、素數表和因子表等若干數表。8～11章是商業上的計算題,如物價、利潤、利息、貨幣換算等，反映了中世紀地中海地區的廣泛商業交往。
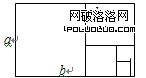
黃金分割的算法：1.如果線段AB被點C分成線段AC和BC，且 ，那麼稱線段AB被點C黃金分割，點C叫做線段AB的黃金分割點，AC與AB的比叫做黃金比。通過計算可知黃金比為
。2.黃金矩形：一個矩形如果兩邊之比具有黃金比值，則稱這種矩形為黃金矩形．它是由一個正方形和另一個小黃金矩形組成。事實上，如圖（4），如果設大黃金矩形的兩邊為a、b，則 
，分出一個正方形後，所余小矩形的兩邊分別為（b－a）和a，它們的比為（b－a）：a
．這表明小的矩形也是黃金矩形。
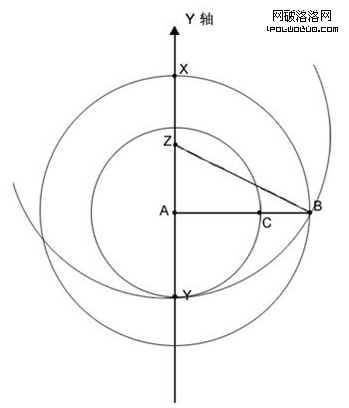
3.如何得到線段的黃金分割點C呢？這裡介紹一下操作方法：首先畫一個參考Y軸（縱軸），如圖所示。A點位於Y軸上，水平畫出AB直線，長度任意。以A為中心，AB為半徑，畫一個圓，得到與Y軸相交的X點。即AX＝AB。取AX的中心點Z，即AZ＝ZX。連接ZB，並以Z為中心，ZB為半徑繪制一個圓，得到與Y軸相交點Y（下方相交點）。即ZB＝ZY。最後，以A為中心點，AY為半徑繪制一個圓，得到與AB相交的C點，此時AC＝AY。C點即為黃金分割點。
鹦鹉螺的曲線黃金分割構圖也體現在網頁構圖上，如titter的IPad版。
三.人物
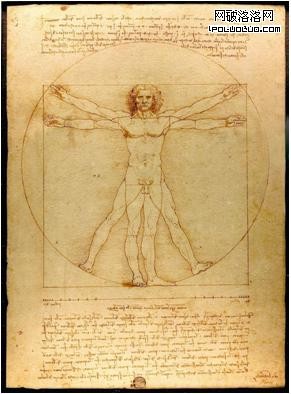
1.面部比例。相貌對不起觀眾的人各有千秋，美麗的人卻有很多相似的地方。奧黛麗赫本有這標准的三平五眼，作為公眾的美女，我們看看他的臉部有那些黃金分割吧。
再以一個普通人鳳姐為例，對比看看，在畫卡通形象的時候可以誇大面部各部分的黃金比例。
2.身體比例
肚臍：頭頂－足底之分割點；(2)咽喉：頭頂－肚臍之分割點；(3)、(4)膝關節：肚臍－足底之分割點；(5)、(6)肘關節：肩關節到中指尖之分割點；(7)、(8)乳頭：軀干乳頭縱軸上這分割點；(9)眉間點：發際到颏底間距上1/3與中下2/3之分割點；(10)鼻下點：發際到下巴底間距下1/3與上中2/3之分割點；(11)唇珠點：鼻底到下巴底間距上1/3與中下2/3之分割點；(12)颏唇溝正路點：鼻底到颏底間距下1/3與上中2/3之分割點；(13)左口角點：口裂水平線左1/3與右2/3之分割點；(14)右口角點：口裂水平線右1/3與左2/3之分割點。（15）在人體中三分之二是水；在22.5 ℃的環境中人體的新陳代謝處於最佳狀態，而22.5 ℃是人體正常體溫36.5 ℃的0.618倍；（16）心髒中心位於胸腔的黃金分割點上；（17）整個脊柱的0.618是胸與腰的分界處，也就是第12胸椎處，從肩至中指指 尖的0.618是肘關節，從肘關節至中指指尖的0.618為腕關節，從膝關節至足尖的0.618是踝關節。（18）姿態優美，身材苗條的時裝模特和翩翩起舞的舞蹈演員，他們的腿和身材的比例也近似於0.618的比值。
思考：如果小明的身高是1.75米，假如肚臍在0.97米位置，增高墊用多高能使肚臍達到人體的黃金分割點？答案最下面公布。
3.另外，和人體有關的黃金分割還有：一年12個月，12的0.618是7.4,7、8月份人體血液中的淋巴細胞最多，它可參與抵御細菌的侵襲，所以這時是人體抵抗力最強的時期。一天中氣溫最低的時間是凌晨2時氣溫最高是在14時，它們之間的黃金分割點為9.4，上午9,10時的氣溫是一天中最適宜的，這時人的頭腦最清楚，辦事效率最高。中醫的三個主要健身穴位棗百會、湧泉和勞宮的位置也符合這一分割律：百會位於前發際至後發際的0.618處，湧泉位於足掌部的0.618處,勞宮位於手掌的0.618處。
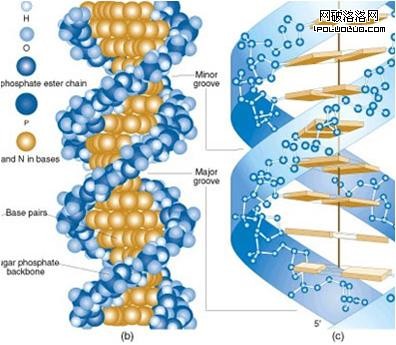
4.DNA的比例。最有意味的是，在人的生命程序DNA 分子中，也包含著“黃金分割比”。它的每個雙螺旋結構中都是由長 34個埃與寬21個埃之比組成的，當然34和21是斐波那契系列中的數字，它們的比率為1.6190476，非常接近黃金分割的1.6180339。這是否說明黃金分割律是比DNA中的遺傳密碼更基本的東西？因為承載DNA的結構——雙螺旋結構——也遵循黃金分割律。
四.建築雕塑
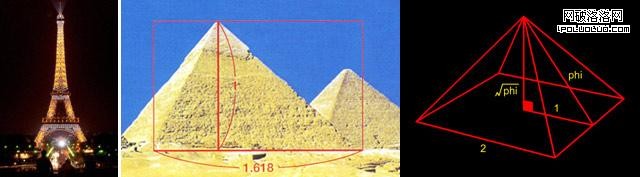
埃菲爾鐵塔是一座紀念性建築物，為了紀念法國大革命100周年，巴黎決定在1889年舉辦國際博覽會，並要造一座永久性紀念建築物。埃菲爾鐵塔在1889年初建時，高度已達300米，是當時全世界最高的建築物，直到1930年，仍是最高的（1959年在埃菲鐵塔頂部增設廣播天線，使塔高增加到320米。） 埃菲爾鐵塔在距離地面57米，115米和276米處，各有一個平台，計算表明：（300-115） 300=0.617。所得比值與黃金比0.618相差甚微，由此可見，埃菲爾鐵塔第二層平台的位置，非常接近於全塔高度的黃金分割點，從圖中可以看出，第二層平台正是埃菲爾鐵塔張開的四條腿開始收攏的轉折點。埃及金字塔的高和底部邊長是黃金比例。
雕塑維納斯的身體各部分也符合黃金比例。
五.繪畫攝影
蒙娜麗莎的微笑
達·芬奇的“美麗密碼”共有六大“法則”，其中包括臉的寬度必須是鼻寬的4倍；前額的寬度、鼻子的長度以及下颌骨長度必須都相等；研究人員吃驚地發現，“六大法則”中的5個都與現代人的審美標准奇跡般地吻合，只有一項關於“鼻子與嘴的比例”的法則與現代略有出入。小巧的嘴型是文藝復興時期的審美標准，嘴的寬度是鼻寬的1.5倍被認為最完美。與之不同的是，研究發現，現代人普遍認為嘴寬與鼻寬的比例達到1.6的更美。達·芬奇的“美麗密碼”要求如此嚴苛，以至於大多數普通人都不能全部符合其標准。因此研究人員也表示：“盡管這一研究結果顯示臉部器官的大小、組合方式以及位置不同，都會對個人魅力產生影響。但一個人的美麗是一個復雜的組合，其中還涉及到其他許多因素。”
攝影的九宮構圖法
九宮構圖顧名思議,將畫面平均九等分,而四個交叉點側是黃金點,拍攝時將主體放在圖中四個交叉點中的任何一個點上,而不是放在畫面的中心或接近中心的位置上.而四個點中,一般認為,右上方的點,是最理想的位置。
六.其他
1.美劇中的黃金分割過場
•盛開的花瓣中隱藏著蜻蜓的翅膀，花心是費馬螺線組成，而螺線的排列與黃金分割和斐波那契數列相關。
•青蛙的背後有希臘文第21個字母PHI(Φ)，這個字母用來代表黃金分割，1.6180339887。
•角的形狀就是斐波納契螺線，而仔細觀察可以看到角上的數字，就是黃金分割數值Phi-Φ——1.6180
•海馬的身上圖形是Fibonacci Spiral斐波納契螺線，同時，螺線裡面包含的線代表了黃金分割的比例。海馬的尾部是Fibonacci Spiral，一些圖片中還包括了L-histidine 組氨酸和L-proline脯氨酸的結構圖。
2.手機界面
•Iphone宮格界面，每個圖標都是57*57，圖標寬度與圖標頂部到下一排圖標的高度的比例是黃金比例。
•天語手機傳統的九宮格形式，對屏幕也進行了視覺上的黃金分割。
•WM6.5的蜂窩系統，六邊形一方面最省空間，一方面也接近於黃金比例的5邊型。
關於黃金分割的總結就告一段落了，一些例子可以靈活的運用到設計當中，希望對看到這篇文章的同學們不管是設計或者PK都有所幫助。
歡迎討論，謝謝：）
PS：小明的答案1.75*0.618-0.97=0.11米