使用canvas繪制貝塞爾曲線
編輯:HTML5教程
1、二次貝塞爾曲線
quadraticCurveTo(cpx,cpy,x,y) //cpx,cpy表示控制點的坐標,x,y表示終點坐標;
數學公式表示如下:
二次方貝茲曲線的路徑由給定點P0、P1、P2的函數B(t)追蹤:
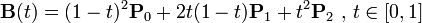
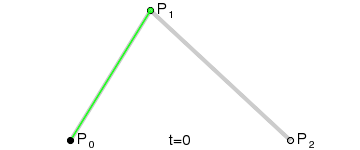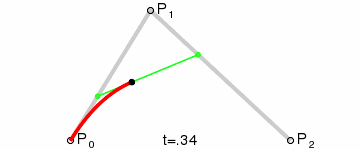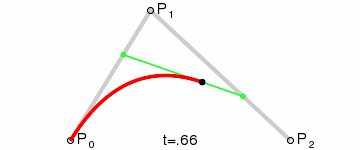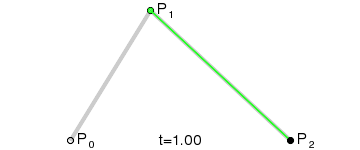
代碼實例:
代碼如下:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>canvas直線</title>
<meta name="Keywords" content="">
<meta name="author" content="@my_programmer">
<style type="text/css">
body, h1{margin:0;}
canvas{margin: 20px;}
</style>
</head>
<body onload="draw()">
<h1>二次貝塞爾曲線</h1>
<canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>
<script>
function draw() {
var canvas=document.getElementById('canvas');
var context=canvas.getContext('2d');
//繪制起始點、控制點、終點
context.beginPath();
context.moveTo(20,170);
context.lineTo(130,40);
context.lineTo(180,150);
context.stroke(); </p> <p> //繪制2次貝塞爾曲線
context.beginPath();
context.moveTo(20,170);
context.quadraticCurveTo(130,40,180,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>
代碼效果:
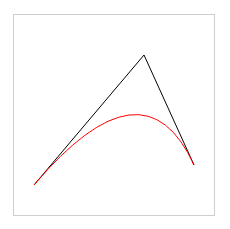
2、三次貝塞爾曲線
bezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y) //cp1x,cp1y表示第一個控制點的坐標,cp2x,cp2y表示第二個控制點的坐標,x,y表示終點的坐標;
數學公式表示如下:
P0、P1、P2、P3四個點在平面或在三維空間中定義了三次方貝茲曲線。曲線起始於P0走向P1,並從P2的方向來到P3。一般不會經過P1或P2;這兩個點只是在那裡提供方向資訊。P0和P1之間的間距,決定了曲線在轉而趨進P3之前,走向P2方向的“長度有多長”。
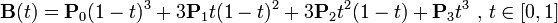
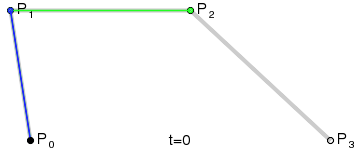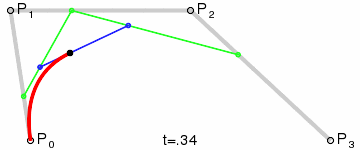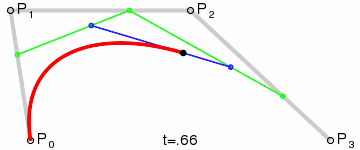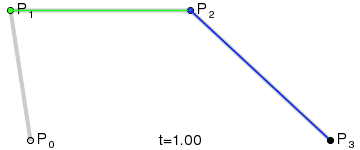
代碼實例:
代碼如下:<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>canvas直線</title>
<meta name="Keywords" content="">
<meta name="Description" content="">
<style type="text/css">
body, h1{margin:0;}
canvas{margin: 20px; }
</style>
</head>
<body onload="draw()">
<h1>三次貝塞爾曲線</h1>
<canvas id="canvas" width=200 height=200 style="border: 1px solid #ccc;"></canvas>
<script>
function draw() {
var canvas=document.getElementById('canvas');
var context=canvas.getContext('2d');
//繪制起始點、控制點、終點
context.beginPath();
context.moveTo(25,175);
context.lineTo(60,80);
context.lineTo(150,30);
context.lineTo(170,150);
context.stroke(); </p> <p> //繪制3次貝塞爾曲線
context.beginPath();
context.moveTo(25,175);
context.bezierCurveTo(60,80,150,30,170,150);
context.strokeStyle = "red";
context.stroke();
}
</script>
</body>
</html>
代碼效果圖:
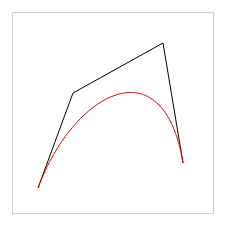
是不是很炫酷的效果。。。HTML5+canvas真是個好玩的東西,上瘾了。
- 上一頁:使用canvas繪制超炫時鐘
- 下一頁:canvas需要在標簽裡直接定義寬高
小編推薦
熱門推薦