一、為什麼要寫這篇文章
某年某月某時某種原因,我在慕課網上看到了一個大神實現了關於小球的拋物線運動的代碼,心中很是欣喜,故而寫這篇文章來向這位大神致敬,同時也為了彌補自己在運動效果和動畫效果制作方面的不足
二、幾種簡單的直線運動
這一部分主要講解的是簡單的運動效果的實現原理,其實所有的canvas動畫效果的實現在核心思想是一致的:都是先定義個初始的狀態,然後定義一個定時器,定時器內執行一個方法,記得在這個方法中要對當前的畫面清除,然後在這個方法中重新繪制需要變化的效果,由於人眼存在殘影,所以短時間內的中斷的變化可以看成是連續的變化,這個就是canva動畫運動原理
最簡單的要從勻速直線運動說起,然後是勻加速直線運動。
勻速直線運動
HTML代碼
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>canvas勻速直線運動</title>
<link rel="stylesheet" type="text/css" href="style.css">
</head>
<body>
<canvas id="canvas">你的浏覽器不支持canvas,請跟換其他浏覽器試一試</canvas>
<script type="text/javascript" src="script.js"></script>
</body>
</html>
JS代碼
window.onload=function(){
var canvas=document.getElementById('canvas');
canvas.height=728;
canvas.width=1024;
var context=canvas.getContext('2d');
context.fillStyle='red';
context.beginPath();
context.arc(800,300,30,0,2*Math.PI,true);
context.closePath();
context.fill();
setInterval(function(){
run(context);
}, 50);
};
var speed=0;
var startPoint=800;
function run(cxt){
speed=-7;
cxt.clearRect(0,0,1024,728);
//cxt.top+=speed;
startPoint+=speed;
cxt.beginPath();
cxt.arc(startPoint,300,30,0,2*Math.PI,true);
cxt.closePath();
cxt.fill();
}
運行效果如下:

PS:這裡面畫面有點卡頓,是錄制的時候軟件的因素造成的,直接運行上訴代碼是可以看到正常運行的效果
重點代碼分析:
var speed=0;
var startPoint=800;
function run(cxt){
speed=-7;
cxt.clearRect(0,0,1024,728);
//cxt.top+=speed;
startPoint+=speed;
cxt.beginPath();
cxt.arc(startPoint,300,30,0,2*Math.PI,true);
cxt.closePath();
cxt.fill();
}
先把速度定義為0和獲取開始點,然後將canvas畫面的內容清除,接著是計算變化後的坐標,然後進行重繪(坐標重新計算是運動關鍵所在)
勻變速直線運動
勻變速直線運動的定義:在直線運動中,把加速度的大小和方向都不改變的運動(加速度為正時),稱之為勻加速直線運動。
基本公式:
速度公式: V=V0+at 位移公式: x=V0t+1/2at^2所以我們依次需要定義這樣的幾個變量加速度a,初始速度V0,位移量x,隨時間變化的速度v,時間time,這幾個變量的初始化值均為0,代碼如下所示:
HTML代碼:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>canvas勻加速直線運動</title>
<link rel="stylesheet" type="text/css" href="style.css">
</head>
<body>
<canvas id="canvas">你的浏覽器不支持canvas,請跟換其他浏覽器試一試</canvas>
<script type="text/javascript" src="script.js"></script>
</body>
</html>
JavaScript代碼:
window.onload=function(){
var canvas=document.getElementById('canvas');
canvas.height=728;
canvas.width=1024;
var context=canvas.getContext('2d');
context.fillStyle='red';
context.beginPath();
context.arc(800,300,30,0,2*Math.PI,true);
context.closePath();
context.fill();
setInterval(function(){
run(context);
}, 50);
};
var v0=0;//初始速度
var a=0;//加速度
var v=0;//變化的速度
var time=0;//時間
var x=0;//位移量
var startPoint=800;//起始點
// V=V0+at
// x=v0t+1/2at^2
// v^2-V^2=2ax
function run(cxt){
time+=0.05;
a=10;
x=-(0.5*a*(time*time));//位移公式代入
startPoint+=x;
cxt.clearRect(0,0,1024,728);
cxt.beginPath();
cxt.arc(startPoint,300,30,0,2*Math.PI,true);
cxt.closePath();
cxt.fill();
}
運行的效果如下:

基本上直線運動比較典型的也就是這兩種,如有遺漏其他運動或者是需要博主講解其他運動的制作的,請在留言板上留言
三、簡單的曲線運動的實現
說到簡單的曲線運動,我們就從最簡單的也是我認為最基礎的運動圓周運動說起
1、勻速圓周運動
圓周運動的定義:質點沿圓周運動,如果在任意相等的時間裡通過的圓弧長度都相等,這種運動就叫做“勻速圓周運動”,亦稱“勻速率圓周運動”。因為物體作圓周運動時速率不變,但速度方向隨時發生變化。所以勻速圓周運動的線速度是每時每刻都在發生變化的。
勻速圓周運動的實現與分析
勻速圓周運動的實現第一反應我們會選擇通過勻速圓周運動的物理公式進行計算得到,但是物理公式中沒有哪條明確的公式是可以把單位時間的變化量和所在點的具體坐標相關聯的,顯然這樣的一條思路是行不通的,從物理公式上面是來說是不具有可行性的,所以我們應該要換另外的一種方法來實現,這個時候我們應該要看透勻速圓周運動的本質,本質上來說,勻速圓周運動的實現其實就是通過一個原點,然後在這個原點的基礎之上對一個物體進行360度的旋轉。好的,相信對canvas api熟悉的小伙伴已經想到了,是的,我們可以通過旋轉或者是矩陣來實現
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>canvas實現圓周運動</title>
<link rel="stylesheet" type="text/css" href="style.css">
</head>
<body>
<canvas id="canvas">你的浏覽器不支持canvas,請跟換其他浏覽器試一試</canvas>
<script type="text/javascript" src="script.js"></script>
</body>
</html>
相關的JavaScript代碼:
window.onload=function(){
var canvas=document.getElementById('canvas');
canvas.height=728;
canvas.width=1024;
var context=canvas.getContext('2d');
drawNotChange(context);
context.fillStyle='blue';
context.beginPath();
context.arc(500,550,30,0,2*Math.PI,true);
context.closePath();
context.fill();
setInterval(function(){
run(context);
}, 50);
};
var time=0;//定義運動的執行次數
function run(cxt){
cxt.clearRect(0,0,1024,728);
drawNotChange(cxt);
cxt.save();//將當前以左上角坐標為(0,0)的上下文環境進行保存,這樣是為了在接下來中要進行畫布偏移後,可以進行還原當前的環境
cxt.translate(500,400);
cxt.rotate(time*8*Math.PI/180);//設定每次旋轉的度數
cxt.fillStyle='blue';
cxt.beginPath();
cxt.arc(0,150,30,0,2*Math.PI,false);
cxt.closePath();
cxt.fill();
cxt.restore();//將當前為(500,400)的點還原為(0,0),其實在save中就是將上下文環境保存到棧中,在restore下面對其進行還原
time+=1;
}
//繪制不變因素
function drawNotChange(context){
context.fillStyle='red';
context.beginPath();
context.arc(500,400,30,0,2*Math.PI,true);
context.closePath();
context.fill();
context.beginPath();
context.arc(500,400,150,0,2*Math.PI,true);
context.closePath();
context.stroke();
}
運行的結果如下:
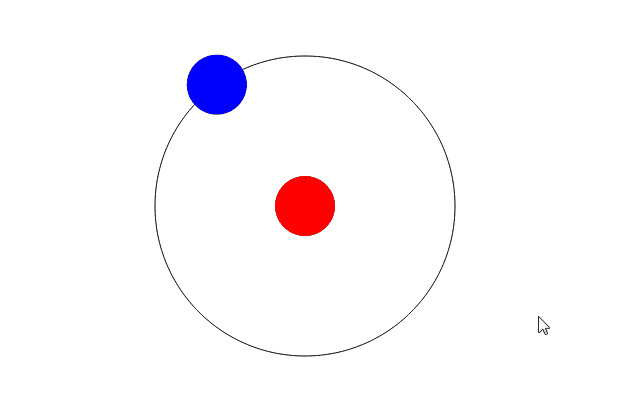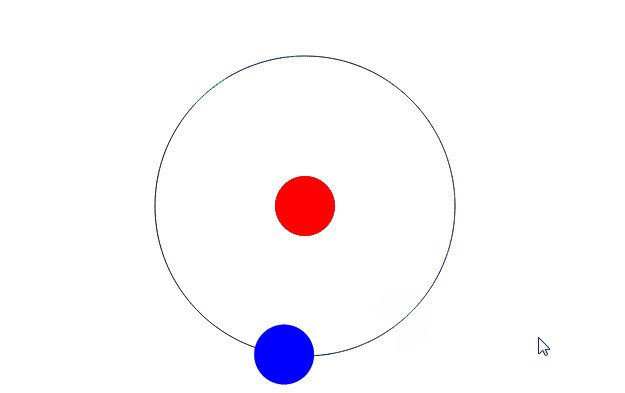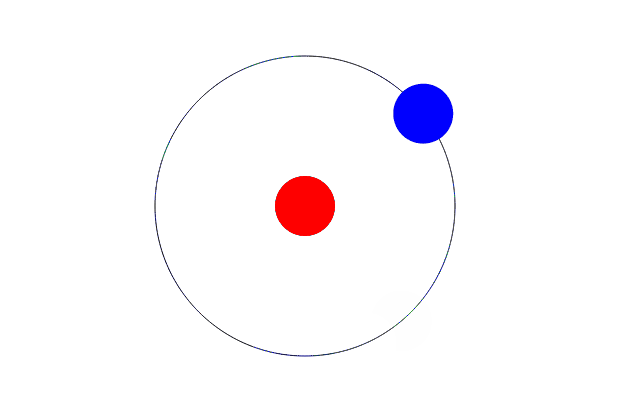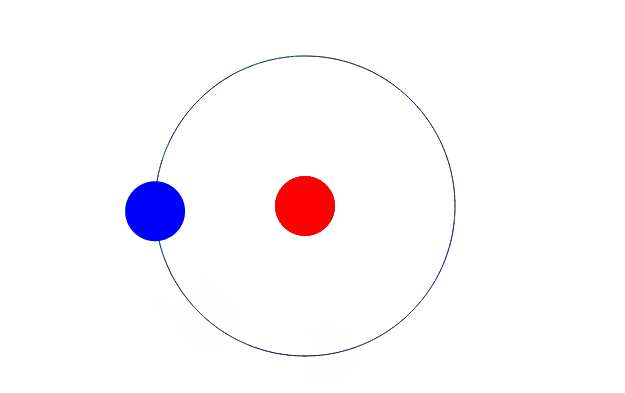
為了讓讀者能夠明白其中的原理,我會在注釋中盡量將代碼注釋清楚
2、橢圓運動
可能有些小伙伴們對於高中的知識都已經遺忘了,但是這個不妨礙,因為在接下來我們會通過一步一步的復習相關數學知識最後才來實現效果,但是如果對高中知識比較熟悉的小伙伴,建議跳過這個階段,直接看代碼就行了,以免浪費時間
橢圓的定義:橢圓(Ellipse)是平面內到定點F1、F2的距離之和等於常數(大於|F1F2|)的動點P的軌跡,F1、F2稱為橢圓的兩個焦點。其數學表表達式為:|PF1|+|PF2|=2a(2a>|F1F2|)
橢圓圖解:
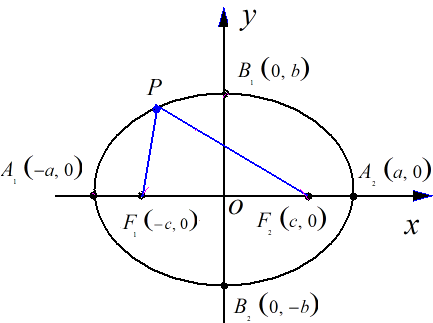
長軸長我們用2a表示,短軸長我們用2b表示
假設橢圓的長軸與X軸平行,那麼表達式如下所示:
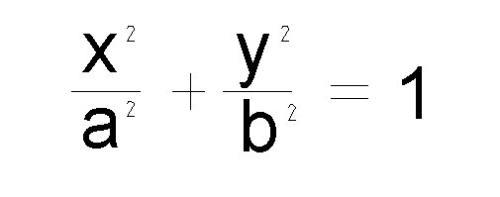
根據三角函數之間的關系我們可以推導出:
x=a+cos(t)
y=b+sin(t)
這裡面的t代表的是單位是單位時間內旋轉的弧度
具體的推導會在以後有時間,為大家專門寫一篇博文來講解一些公式的推導過程
關於橢圓的數學知識已經講完了,還是不太清楚的同學請執行去復習高中的知識,在這裡就不再累贅了。
我們還開始代碼實現之前還有先假設好一些參數,我們假設原點O(500,300),繞橢圓運動的物體為圓形半徑為30,其中長半軸長a=200,短半軸長為b=100,每次重新獲取物體的運動後的移動位置的時候,x都會變化一個單位,旋轉為順時針旋轉,開始位置為原點的正左邊的端點,最後原點我們以一個黑色且半徑為10的小球表示。注意:上述的數據可以讀者自行定義,但是要注意這個前提是必須保證a>b,如果a<b那麼就不是這個公式了
我們先來實現橢圓的軌跡效果:
HTML代碼:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>canvas實現橢圓運動</title>
<link rel="stylesheet" type="text/css" href="style.css">
</head>
<body>
<canvas id="canvas">你的浏覽器不支持canvas,請跟換其他浏覽器試一試</canvas>
<script type="text/javascript" src="script.js"></script>
</body>
</html>
JavaScript代碼:
var a=200,
b=100,
radius=30;
window.onload=function(){
var canvas=document.getElementById('canvas');
canvas.height=668;
canvas.width=1024;
var cxt=canvas.getContext('2d');
cxt.beginPath();
cxt.arc(300,300,10,0,2*Math.PI,true)
cxt.closePath();
cxt.fill();
route(cxt,300,300,200,100);
};
//橢圓路線繪制
function route(context,x,y,a,b){
//max是等於1除以長軸值a和b中的較大者
//i每次循環增加1/max,表示度數的增加
//這樣可以使得每次循環所繪制的路徑(弧線)接近1像素
var step = (a > b) ? 1 / a : 1 / b;
context.beginPath();
context.moveTo(x + a, y); //從橢圓的左端點開始繪制
for (var i = 0; i < 2 * Math.PI; i += step)
{
//參數方程為x = a * cos(i), y = b * sin(i),
//參數為i,表示度數(弧度)
context.lineTo(x + a * Math.cos(i), y + b * Math.sin(i));
}
context.closePath();
context.stroke();
}
橢圓的軌跡的思路是:通過循環,將極小的線段首尾相連,繪制了一個類似於橢圓的一個圖像,但是由於線段太過細小導致了我們肉眼看上去就成了一個橢圓
運行的效果是:
橢圓上小球的運動實現
這個的制作思路跟上面的思路是一樣的,所以這裡就不再分析
這次我們就先看一看效果如何:
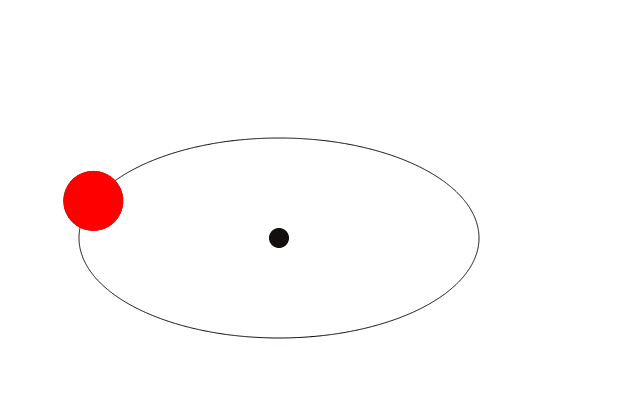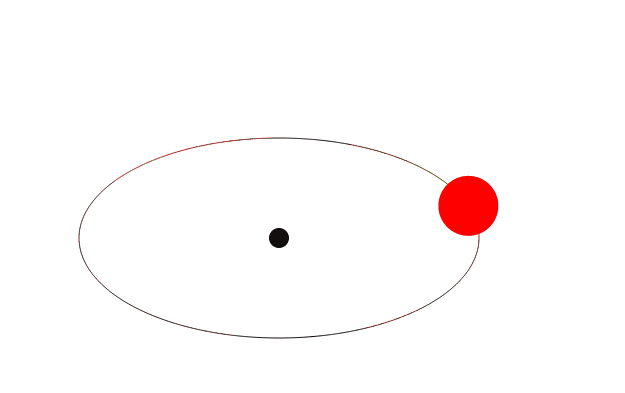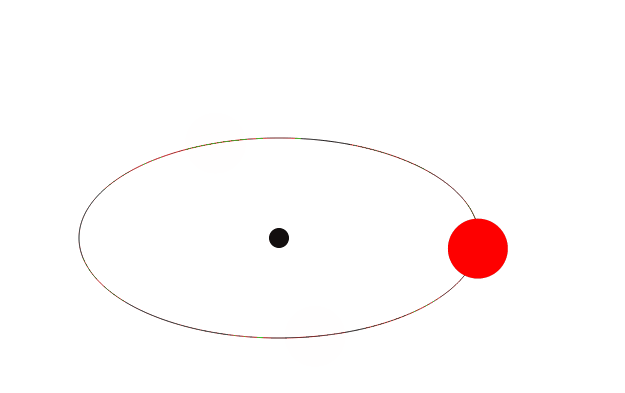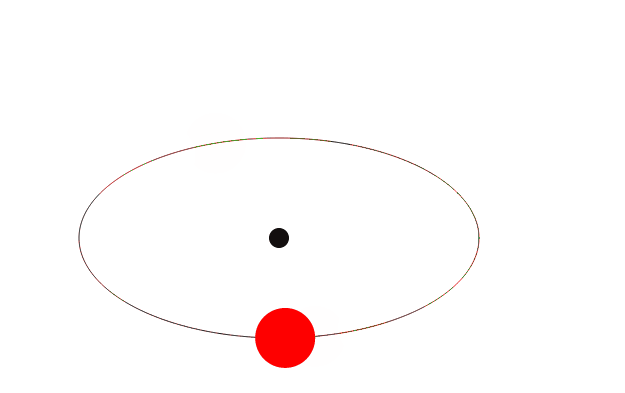
HTML代碼和上面的例子相同
JavaScript代碼如下:
var a=200,
b=100,
radius=30;
time=0;//循環的次數
window.onload=function(){
var canvas=document.getElementById('canvas');
canvas.height=768;
canvas.width=1024;
var cxt=canvas.getContext('2d');
centerPoint(cxt);
arcRoute(cxt,300,300,a,b,radius);
setInterval(function(){
arcRoute(cxt,300,300,a,b,radius);
}, 70);
};
//繪制原點
function centerPoint(cxt){
cxt.fillStyle="black";
cxt.beginPath();
cxt.arc(300,300,10,0,2*Math.PI,true)
cxt.closePath();
cxt.fill();
}
//橢圓路線繪制
function route(context,x,y,a,b){
var step = (a > b) ? 1 / a : 1 / b;
context.beginPath();
context.moveTo(x + a, y); //從橢圓的左端點開始繪制
for (var i = 0; i < 2 * Math.PI; i += step)
{
context.lineTo(x + a * Math.cos(i), y + b * Math.sin(i));
}
context.closePath();
context.stroke();
}
//橢圓上小球運動的實現
function arcRoute(context,x,y,a,b,r){
context.clearRect(0,0,1024,768);
route(context,x,x,a,b);
centerPoint(context);
var step = (a > b) ? 1 / a : 1 / b;
context.fillStyle="red";
if(time==0){
context.beginPath();
context.arc(x,y,r,0,2*Math.PI,true);
context.closePath();
context.fill();
}else{
context.beginPath();
context.arc(x+a*Math.cos(time),y+b*Math.sin(time),r,0,2*Math.PI,true);
context.closePath();
context.fill();
}
time+=1;
}
四、相關的參考資料
火狐開發者中心
沈佳洋
好了,這一節的內容就先結束了,下一節預告,下一節:會談談一些其他的運動效果的實現和這些運動效果的另一種實現方式,同時還會有一些關於碰撞的檢測等等的知識,敬請期待。如果有什麼不懂或者是錯誤的地方,歡迎給位朋友在留言板留下你的想法,你的支持是我前進的動力