DIV CSS 佈局教程網

上一篇文章講了canvas的arc方法，這一篇講和他有關的arcTo方法。 
arc與arcTo，從名字都能看出來相似。arcTo也是畫曲線的方法，而且他畫出的曲線也是正圓的一段弧線。但他的參數和arc簡直是不共戴天~ 
ctx.arcTo(x1,y1,x2,y2,radius);arcTo的參數中包括兩個點，而且這兩個點中並沒有表示圓心的點，僅僅最後的參數是圓的半徑，表示arcTo和圓有那麼點關系。 
網上關於arcTo的文章很少，好不容易找到一篇還是外國的；而且canvas畫圖木有直觀工具，只能靠猜，arcTo害我猜了半天。。 
為了直觀的描述，我采取了一種輔助辦法：arcTo畫到哪裡，我就用lineTo也畫到相應的點，以查看他們的關系。就是畫輔助線。 

復制代碼代碼如下:www.mb5u.com
var x0=100, 
y0=400, 
x1 = 500, 
y1 = 400, 
x2 = 450, 
y2 = 450; 
ctx.beginPath(); 
ctx.moveTo(x0,y0); 
ctx.strokeStyle = "#f00"; 
ctx.lineWidth = 2; 
ctx.arcTo(x1,y1,x2,y2,20); 
ctx.stroke(); 
ctx.beginPath(); 
ctx.strokeStyle = "rgba(0,0,0,0.5)"; 
ctx.lineWidth = 1; 
ctx.moveTo(x0,y0); 
ctx.lineTo(x1,y1); 
ctx.fillText('x1,y1',x1+10,y1+10) 
ctx.lineTo(x2,y2); 
ctx.fillText('x2,y2',x2+10,y2) 
ctx.stroke(); 

看起來代碼有點多，其實很簡單。我用了幾個變量來保存坐標值，其余的都是canvas的操作了。 
變量說明：x0,y0是起點坐標，x1,y1是第一個點坐標，x2,y2就是第二個點坐標。其中lineTo畫的直線是半透明的1px黑線，arcTo畫的線條是2px的紅線。 
刷新頁面，即可看到下圖。 

不得不說這條紅線很像一個鉤子。 
於是arcTo的規律就找到了，他其實是通過起點，第1點，第2點的兩條直線，組成了一個夾角，而這兩條線，也是參數圓的切線。 
其中圓的半徑決定了圓會在什麼位置與線條發生切邊。就像一個球往一個死角裡面滾，球越小就滾得越進去，越靠近死角；球大則反之。 
這是一個很嚴肅的學術問題，大家可不要YY。 
讓我們把球球變大吧！ 

復制代碼代碼如下:www.mb5u.com
ctx.arcTo(x1,y1,x2,y2,50); //半徑改成50 

如圖，你可以看到圓弧變得很大，甚至都不和直線相切了。 
當然，實際上他們還是相切的，因為切線是無限延長的。 
我們繼續探索，把圓繼續變大，把起點與第1點的距離縮短。 

復制代碼代碼如下:www.mb5u.com
var x0=400; //起點x坐標從100變400 
... 
ctx.arcTo(x1,y1,x2,y2,100); //圓的半徑變大到100然後你就會看到這麼個奇特的圖形。 

本來是個鉤子，現在被硬生生的掰彎了，還掰到反方向了！有點像酒瓶架了。 
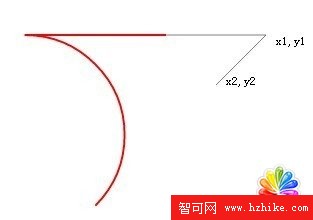
不過，大家注意看，這個圓依然是和兩條線相切的！只是現在兩條線的長度都滿足不了這個圓了！他已經把兩條線都無線延長了！ 
這個鉤子柄什麼時候會發生反轉呢？如果你幾何學的好，你可以試著理解一下點與圓的切線方程。 
arcTo方法中有個很重要的點，這個重要的點就是代碼中的(x1,y1),只要他到圓的切點的距離，超過了他到起點(x0,y0)的距離，就會發生反轉。 
從圖中我們可以看到，(x2,y2)這個點的坐標可以無限變化，只要他始終是切線上的一個點，那麼在圓的半徑不變的情況下，arcTo畫出的圖形不會有任何變化。這點需要特別注意。 
讓我用我拿不上台面的幾何知識來驗證下這個命題吧。為了方便計算，我先把兩條線的夾角改成90度。 

復制代碼代碼如下:www.mb5u.com
var x0=100, 
y0=400, 
x1 = 500, 
y1 = 400, 
x2 = 500, 
y2 = 450; 

更改後就是90度張開了喲！我們保持球的半徑不變。刷新後： 

我們把y2變大，也就是延長了一條切線，把他變成550，刷新後：

 
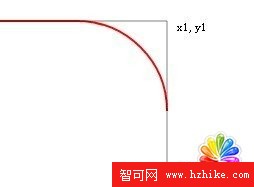
切線是延長了，但arcTo畫出的紅線沒有任何變化。