一.簡介

在3D編程的中，我們利用向量與矩陣的運算來簡化空間坐標變換的計算，比如求出某立方體繞任意軸旋轉後的坐標，再比如計算旋轉+縮放+切變+投影後的坐標變換，如果拋棄矩陣，將陷入大量的復雜計算當中。利用齊次坐標技術來描述空間各點的坐標，用4*4的矩陣來解決空間各點的變換，已經成了計算機圖形學的一個標准。

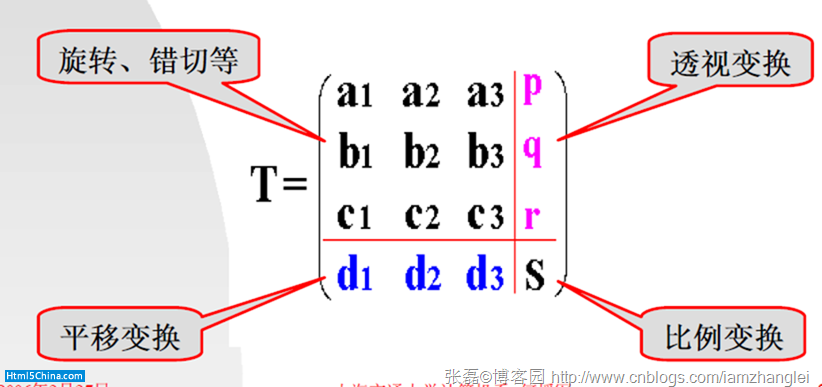
比如主流的3D APIs如OpenGL、微軟的Direct3D，還有Javascript版的3D引擎Three.JS,還有Glide、Heidi等等，

基於這些API之上的API有Java3D,XNA framework。我們在msdn官網的xna api上可以看到這張圖，可以看到4*4的矩陣。

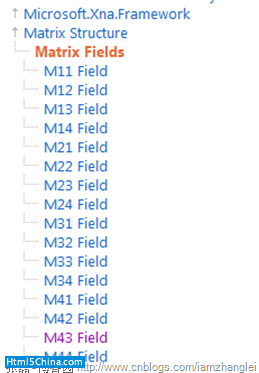
二.投影矩陣

我們先來揭開投影矩陣的神秘面紗。

矩陣中各個變量值的意義如下圖所示：

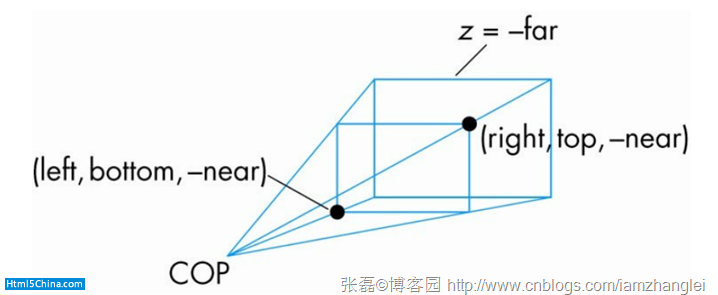
然後我從Three.JS上拔下一段代碼：

JavaScript Code復制內容到剪貼板

1. THREE.Matrix4.makeFrustum = function ( left, right, bottom, top, near, far ) {  
2.        
3.         var m, x, y, a, b, c, d;  
4.        
5.         m = new THREE.Matrix4();  
6.        
7.         x = 2 * near / ( right - left );  
8.         y = 2 * near / ( top - bottom );  
9.        
10.         a = ( right + left ) / ( right - left );  
11.         b = ( top + bottom ) / ( top - bottom );  
12.         c = - ( far + near ) / ( far - near );  
13.         d = - 2 * far * near / ( far - near );  
14.        
15.         m.n11 = x;  m.n12 = 0;  m.n13 = a;   m.n14 = 0;  
16.         m.n21 = 0;  m.n22 = y;  m.n23 = b;   m.n24 = 0;  
17.         m.n31 = 0;  m.n32 = 0;  m.n33 = c;   m.n34 = d;  
18.         m.n41 = 0;  m.n42 = 0;  m.n43 = - 1; m.n44 = 0;  
19.        
20.         return m;  
21.        
22.     };  

沒錯，它就是投影變換矩陣。為了能夠看得懂這個矩陣，那麼就要從頭說起·········

三.什麼是矩陣

數學上，一個m×n矩陣乃一m行n列的矩形陣列。矩陣由數組成，或更一般的，由某環中元素組成。

矩陣常見於線性代數、線性規劃、統計分析，以及組合數學等。請參考矩陣理論。

以下是一個4 × 3矩陣：

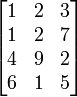
某矩陣A的第i 行第j 列，或i,j位，通常記為A[i,j] 或Ai,j。在上述例子中A[2,3]=7。

此外A = (aij)，意為A[i,j] = aij對於所有i及j，常見於數學著作中。

四.向量和矩陣的乘積

為了搞明白向量和矩陣的運算，首先來看單位向量和矩陣的乘積，我們拿行式（也可以用列式）為例。

我們假設三維的單位坐標向量分別為i=(1,0,0),j=(0,1,0),k=(0,0,1),

我們取x坐標軸上的單位向量i與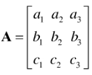相乘。乘積如下：

 

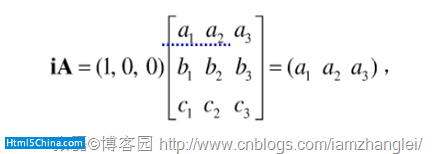
我們取x坐標軸上的單位向量j與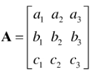相乘。乘積如下：

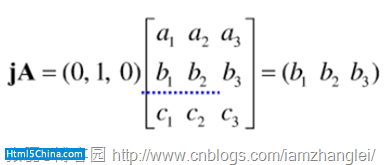
我們取x坐標軸上的單位向量k與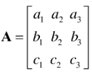相乘。乘積如下：

 

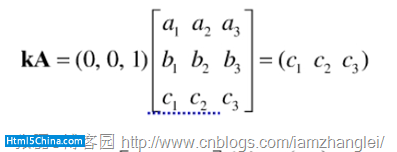
所以如果我們用向量（1，1，1）與A相乘，最後得到的坐標就是（a1+b1+c1, a2+b2+c2, a3+b3+c3）。 

五.基本初等矩陣的幾何意義

要想理解矩陣的意義，就要從它的幾何意義開始體會，基本初等矩陣有下面三種幾何意義：

(1)關於某一“標准軸（面）”的鏡面反射（對稱）變換

 

 

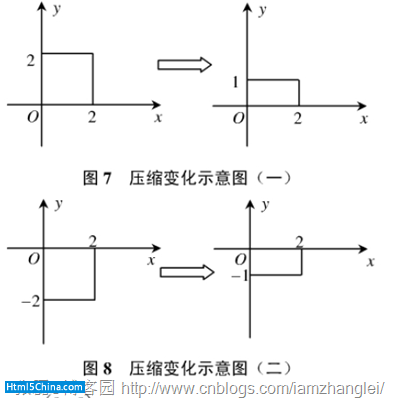
(2)在某一坐標軸方向的伸縮變換（當某一坐標縮小為0時，即投影變換）

 

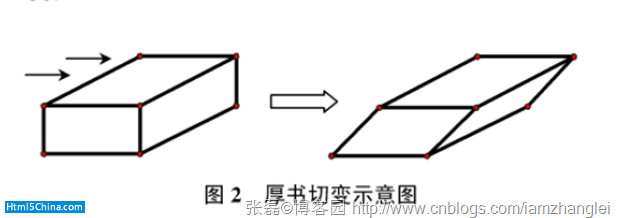
(3)在某一坐標軸方向的切變變換

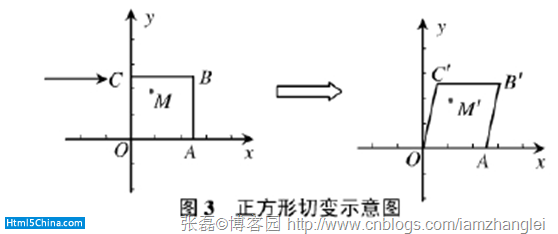
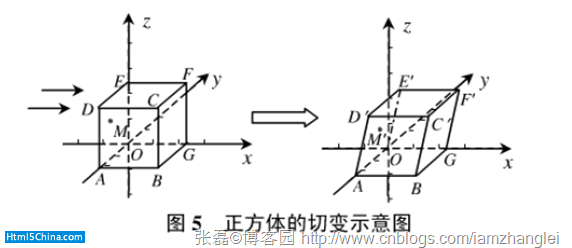
六.神馬是齊次坐標，為什麼要用它？

“齊次坐標表示是計算機圖形學的重要手段之一，它既能夠用來明確區分向量和點，同時也更易用於進行仿射（線性）幾何變換。”—— F.S. Hill, JR

 用於表示n維透視空間的點的n+1維分量。透視空間的點可以被認為是歐幾裡德空間加上一些無窮遠處的點。由於每個坐標分量乘以一個非零值並不改變這些坐標所表示的點，

這樣的坐標是齊次坐標。齊次坐標主要應用在透視幾何計算，因此在場景必須投影到一個窗口上的計算機圖形學中也十分有用。

   為了能用矩陣的形式統一描述圖形變換，在計算機圖形學中常采用齊次坐標的形式來描述空間的點。

    在n維空間中的一個問題，在n+1維空間中相應地也有一個問題，而在n+1維空間中卻常常比n維空間中較易獲得結果。

    二維點（x,y）的齊次表示是（hx,hy,h），這裡h是任何一個非零因子，有時叫做比例因子。

    齊次點（a,b,c）被投射回復到二維時簡單地就是（a/c,b/c）,由比例因子c去除。

在計算機中處理一個三維空間的“無窮遠點”是困難的，但是可以容易地處理一個四維齊次空間的解析點，

例如可以用向量： 

    （1 0 0 0） 表示x軸方向無窮遠點

    （0 1 0 0） 表示y軸方向無窮遠點

    （0 0 1 0） 表示z軸方向無窮遠點

    （0 0 0 1） 表示坐標原點

     這4個向量將構成四維齊次空間的單位矩陣

那麼，我們為什麼要使用齊次坐標呢？

對於一個普通坐標的點P=(Px, Py, Pz)，有對應的一族齊次坐標(wPx, wPy, wPz, w)，其中w不等於零。

比如，P(1, 4, 7)的齊次坐標有(1, 4, 7, 1)、（2, 8, 14, 2）、（-0.1, -0.4, -0.7, -0.1）等等。

因此，如果把一個點從普通坐標變成齊次坐標，給x,y,z乘上同一個非零數w，然後增加第4個分量w；如果把一個齊次坐標轉換成普通坐標，把前三個坐標同時除以第4個坐標，然後去掉第4個分量。由於齊次坐標使用了4個分量來表達3D概念，使得平移變換可以使用矩陣進行，從而如F.S. Hill, JR所說，仿射（線性）變換的進行更加方便。由於圖形硬件已經普遍地支持齊次坐標與矩陣乘法，因此更加促進了齊次坐標使用，使得它似乎成為圖形學中的一個標准。

當顯示器或者照相機拿到這個坐標信息去渲染（渲染的算法先不考慮）的時候，無法得知深度信息，

即z的大小，就得不出非常有層次感立體感的圖片。

所以我們利用齊次坐標技術來描述空間各點的坐標，用4*4的矩陣來解決空間各點的變換。

總結：齊次坐標在投影矩陣中的作用就是對x,y進行縮放，達到透視變換的作用，使得相同的x,y，因為z的不同，投影出的坐標也不同。

七.攝像機的視野

這是我們上次漏掉的一個重要概念，屬於攝像機的一個重要屬性。

我們都有這樣的經驗，當我們正前方看過去的時候，處於我們視野外的東西是看不到的，或者模糊的。所以在3D編程當中，我們要規定

攝像機的視野。如果您玩過《反恐精英》這款游戲的畫，你肯定見過下面這張圖

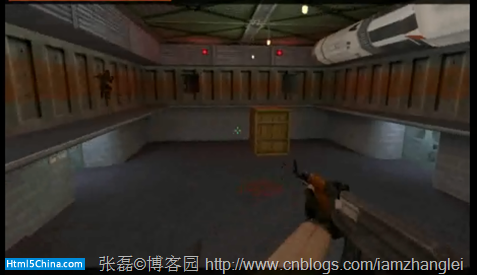
持槍者，有著自己的視野，太靠右邊或者太靠著左邊都看不到，後面就更不用說了。如果我們要把槍口指向右邊，我們就可以

旋轉世界（或者旋轉攝像機）。我們可以根據x,y坐標進行裁剪，裁剪出我們視野中的圖像。

 

 

 

 

 

 

八.透視變換

講透視變換之前，先看一看投影的分類，如下圖：

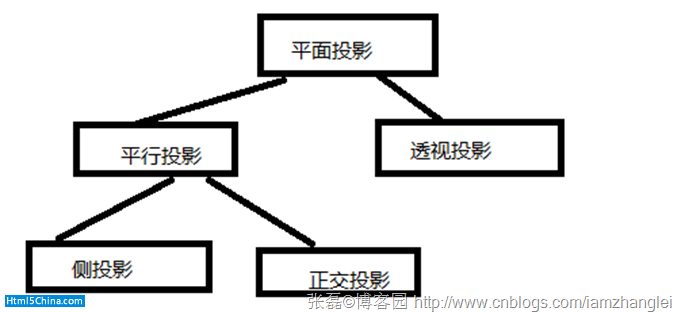
我們所看到的有立體層次感的圖片就是透視投影的結果。

空間裡的坐標，經過透視變換，x,y也會進行一定比例的變化。這也是為什麼Y坐標相等的兩個點，為什麼Z越大，透視投影之後Y越小的原因。

由於，投影的時候，Z的坐標為0，只取X,Y進行渲染。然後透視變換是3D轉2D的必經流水線。而該流水線，就是要取得Z的坐標，對圖形就行渲染。

而這個渲染的過程是在CVV當中進行，也就是一個正方體。在該正方體當中，Z已經不再是Z,但也沒有完全抹去，它也隨著攝像機與屏幕與被觀察物體三者的距離的變化而進行著相應的變化。

投影變換就做一件事：將錐形的觀察空間轉化為單位立方體空間。

下面兩張圖分別代表了透視投影和平行投影：

透視投影：

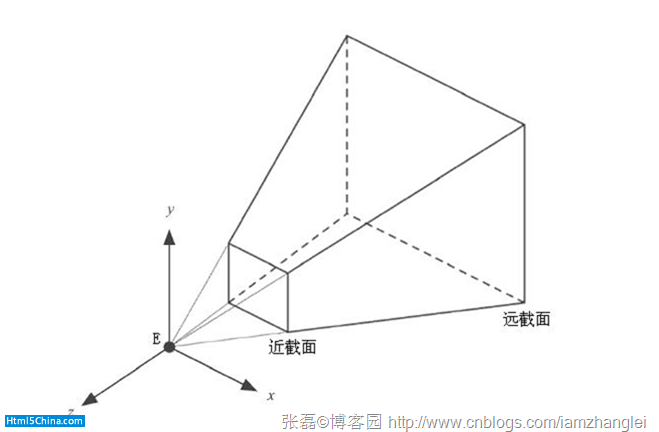
平行投影：

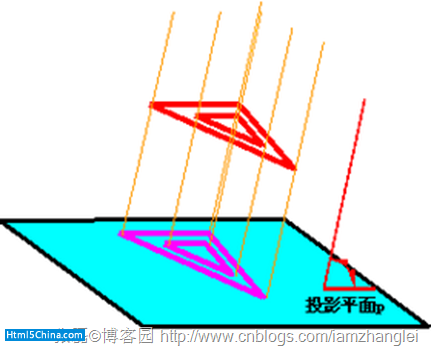
拿上篇文章的演示作為透視例子，如下圖：

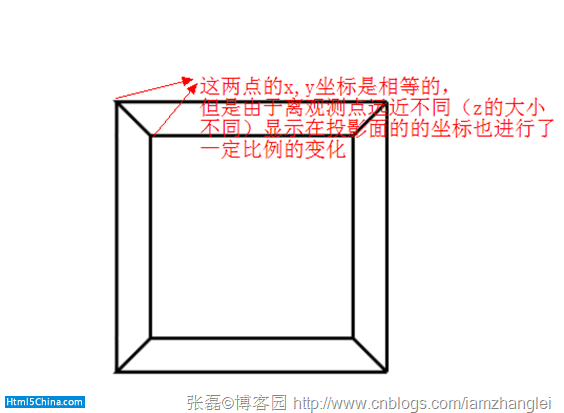
這就是透視變換，這也更加說明了齊次坐標在透視投影中的作用。如果是平行投影，我們看到的就只是一個正方行：

 

 

 

 

九.投影規范化

投影規范化的目的：

1.不想為每種類型的投影設計不同的投影矩陣，所以把所有的投影轉化為具有默認視景的正交投影；

2.這種策略可以使我們在流水線中應用標准變換，並進行有效的裁剪。

投影規范化過程：

1.把對象進行變形，使得變形後的對象經過正交投影後得到與原對象的理想投影一樣的視圖；

2.規范化矩陣就是正交投影矩陣乘上對象變形矩陣。

流水線如下圖：

 

 

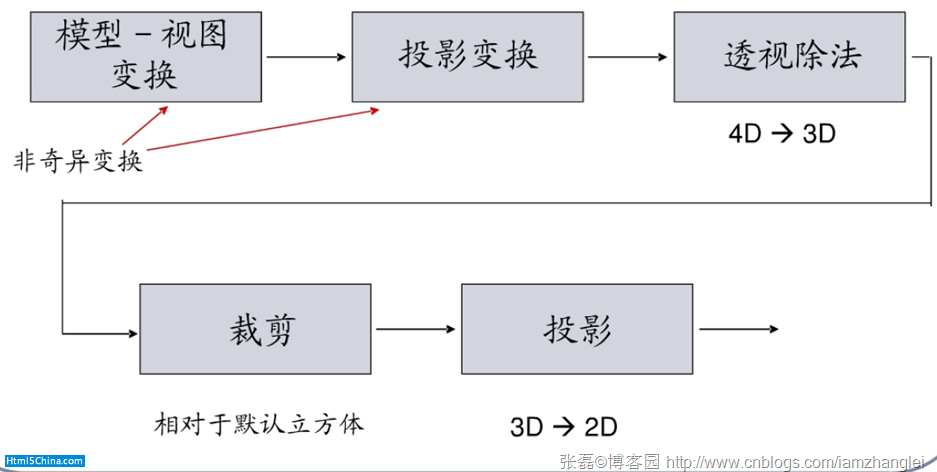
OpenGL、微軟的Direct3D都要經過規范化的投影流水線，而他們之間的區別在於視景立方體的大小，

OpenGL的視景體是邊長為2的正方體，Direct3D的視景體一個是長寬高分別為2，2，1的長方體。

如下圖OpenGL透視投影變換過程：

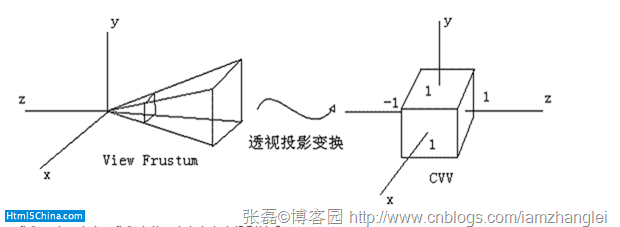
被觀察體上的點和屏幕上的點分別被映射到立方體的前後兩個面，即z=1和z=-1兩個面上，如下圖

 

 

 

 

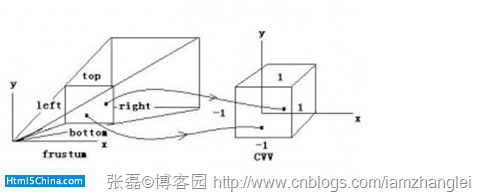
十.投影逆變換

投影逆變化的實際應用中的意義：

我們思考這樣一個問題，先看下面這張圖：

當我們點擊最上面這個藍色的立方體的時候，我們可能也點擊到了下面那個，因為因為他們投影重疊了。

那麼計算機是怎麼知道我們點擊的是上面這個還是下面這個呢？這個大家先思考，已經超過本節范圍，下次詳細分解。

十一.在線演示

a.旋轉矩陣變換

JavaScript Code復制內容到剪貼板

1. function transform() {  
2.             angle = degToRad(currentAngle4)  
3.             init4();  
4.             m4.n11 = Math.cos(angle);  
5.             m4.n13 = -Math.sin(angle);  
6.             m4.n31 = Math.sin(angle);  
7.             m4.n33 = Math.cos(angle);  
8.             for (var i = 0; i < Points4.length; i++) {  
9.            Points4[i]=  m4.multiplyVector4(Points4[i]);  
10.        }  

     

 

b.移動矩陣變換

JavaScript Code復制內容到剪貼板

1. function transform() {  
2.                 angle = degToRad(currentAngle4)  
3.                 init4();  
4.                 m4.n41++;  
5.                 m4.n42++;  
6.                 m4.n43++;  
7.                 for (var i = 0; i < Points4.length; i++) {  
8.                Points4[i]=  m4.multiplyVector4(Points4[i]);  
9.            }  

     

 

c.切變

JavaScript Code復制內容到剪貼板

1. function transform() {  
2.          angle = degToRad(currentAngle4)  
3.          init4();  
4.          m4.n21+=0.01;          
5.          for (var i = 0; i < Points4.length; i++) {  
6.         Points4[i]=  m4.multiplyVector4(Points4[i]);  
7.     }  

   

 

d.比例變換

JavaScript Code復制內容到剪貼板

1. function transform() {  
2.         angle = degToRad(currentAngle4)  
3.         init4();  
4.         m4.n11 += 0.01;  
5.         m4.n22 += 0.01;  
6.         m4.n33 += 0.01;        
7.         for (var i = 0; i < Points4.length; i++) {  
8.        Points4[i]=  m4.multiplyVector4(Points4[i]);  
9.    }