DIV CSS 佈局教程網

這篇文章主要介紹了使用Html5的Canvas繪制曲線的簡單方法,是Html5入門學習中的基礎知識,需要的朋友可以參考下

Canvas2D自帶的曲線方法
　　最近在研究3D柔體的計算，所以在狂補一些知識。經常會涉及到一些數值分析方面的東西，主要是曲線的各種插值算法。突然想起了Canvas2D本身也是可以繪制曲線的，使用的是二次和三次的貝茲曲線。其實我也一直沒用它的過這個方法，現在就來試試吧～
　　這篇只是說說簡單的曲線繪制，咱就不說一大堆復雜的原理了。況且貝茲曲線這東西的原理本身很簡單，看看維基百科就能明白。其實很多繪圖工具中的簡單曲線繪制都是使用貝茲曲線的，如果你用過windows自帶繪圖工具中的曲線就一定不陌生。可以先拖出一條直線，然後點擊某個位置讓直線扭曲。一開始的拖動動作就是決定曲線的兩個頂點，點擊動作就是添加中間點。在Windows自帶的繪圖工具使用的是三次貝茲曲線，你可以添加兩個中間點。貝茲曲線和一般的多項式插值不同，它的中間點只是作為控制點用的，並不是曲線必須經過的頂點。而且它還可以做出閉曲線。Canvas2D中有提供兩個繪制曲線的方法
　　　　quadraticCurveTo：二次貝茲曲線
　　　　bezIErCurveTo：三次貝茲曲線
　　線條是從當前所在位置開始畫的，可以用moveTo方法來指定當前位置。有了曲線的開始位置後，還需要中間點和結束位置。把這些位置坐標傳給繪制函數即可。比如二次貝茲曲線需要一個中間點和一個結束位置，所以要傳兩個坐標給quadraticCurveTo函數。坐標是由x和y組成的，也就是說這個函數有4個參數。bezIErCurveTo也是一樣的，只是它有兩個中間點而已。下面咱就來用用看

CSS Code復制內容到剪貼板

1. <canvas id="canvas" width="200" height="200"></canvas>   
2. <script>   
3. var g=canvas.getContext("2d");   
4. //普通的直線   
5. g.beginPath();   
6. g.strokeStyle="#CCC";   
7. g.moveTo(0,0);   
8. g.lineTo(200,0);   
9. g.lineTo(0,200);   
10. g.lineTo(200,200);   
11. g.stroke();   
12. //貝茲曲線   
13. g.beginPath();   
14. g.strokeStyle="#F00";   
15. g.moveTo(0,0);   
16. g.bezIErCurveTo(200,0, 0,200, 200,200);   
17. g.stroke();   
18. </script>  

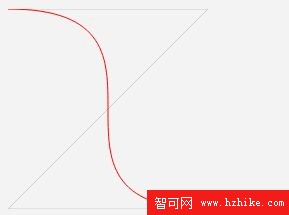
這個按照Z字形的軌跡給定四個點，畫出了普通的直線和貝茲曲線。這只是普通的曲線而已，貝茲曲線的厲害之處是它可以畫出閉曲線，比如這樣一段代碼

CSS Code復制內容到剪貼板

1. g.beginPath();   
2. g.strokeStyle="#00F";   
3. g.moveTo(100,0);   
4. g.bezIErCurveTo(-100,200, 300,200, 100,0);   
5. g.stroke();  

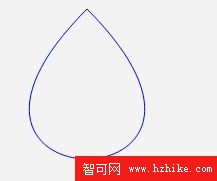
把三次貝茲曲線的開始位置和結束位置設置到同一點上就可以畫出閉曲線。因為貝茲曲線的插值方向不是按照坐標軸走的，所以可以繪制出閉曲線。如果想讓多項式插值繪制出閉曲線我們就得轉換參數，使用極坐標系來完成。
　　我使用的例子都是三次貝茲曲線。其實二次的也一樣，只是少了個中間點就畫不出我想要的東西了。我就不再嗦一大堆了，這篇就這樣吧= =。。