快速排序作為一種高效的排序算法被廣泛應用,SUN的JDK中的Arrays.sort 方法用的就是快排。
快排采用了經典的分治思想(divide and conquer):
Divide:選取一個基元X(一般選取數組第一個元素),通過某種分區操作(partitioning)將數組劃分為兩個部分:左半部分小於等於X,右半部分大於等於X。
Conquer: 左右兩個子數組遞歸地調用Divide過程。
Combine:快排作為就地排序算法(in place sort),不需要任何合並操作
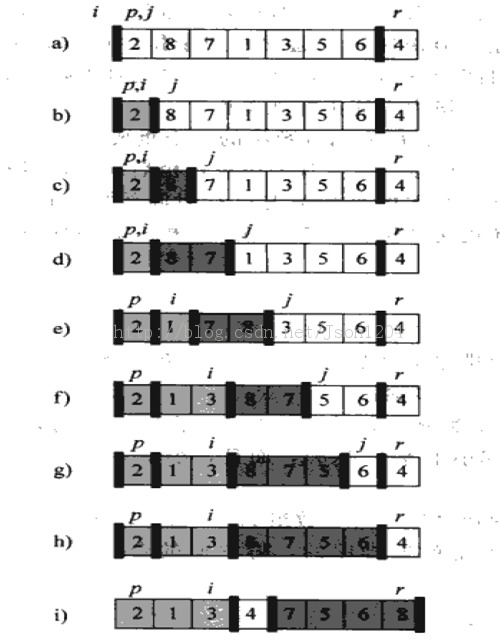
可以看出快排的核心部分就是劃分過程(partitioning),下面以一個實例來詳細解釋如何劃分數組(圖取自於《算法導論》)
初始化:選取基元P=2,就是數組首元素。i=1,j=i+1=2 (數組下標以1開頭)
循環不變量:2~i之間的元素都小於或等於P,i+1~j之間的元素都大於或等於P
循環過程:j 從2到n,考察j位置的元素,如果大於等於P,就繼續循環。如果小於P,就將j位置的元素(不應該出現在i+1~j這個區間)和i+1位置(交換之後仍在 i+1~j區間)的元素交換位置,同時將i+1.這樣就維持了循環不變量(見上述循環不變量說明)。直到j=n,完成最後一次循環操作。
要注意的是在完成循環後,還需要將i位置的元素和數組首元素交換以滿足我們最先設定的要求(對應圖中的第i步)。
細 心的讀者可能會想到另一種更直白的分區方法,即將基元取出存在另一相同大小數組中,遇到比基元小的元素就存儲在數組左半部分,遇到比基元大的元素就存儲在 數組右半部分。這樣的操作復雜度也是線性的,即Theta(n)。但是空間復雜度提高了一倍。這也是快排就地排序的優勢所在。
復制代碼 代碼如下:
public class QuickSort {
private static void QuickSort(int[] array,int start,int end)
{
if(start<end)
{
int key=array[start];//初始化保存基元
int i=start,j;//初始化i,j
for(j=start+1;j<=end;j++)
if(array[j]<key)//如果此處元素小於基元,則把此元素和i+1處元素交換,並將i加1,如大於或等於基元則繼續循環
{
int temp=array[j];
array[j]=array[i+1];
array[i+1]=temp;
i++;
}
}
array[start]=array[i];//交換i處元素和基元
array[i]=key;
QuickSort(array, start, i-1);//遞歸調用
QuickSort(array, i+1, end);
}
}
public static void main(String[] args)
{
int[] array=new int[]{11,213,134,44,77,78,23,43};
QuickSort(array, 0, array.length-1);
for(int i=0;i<array.length;i++)
{
System.out.println((i+1)+"th:"+array[i]);
}
}
}