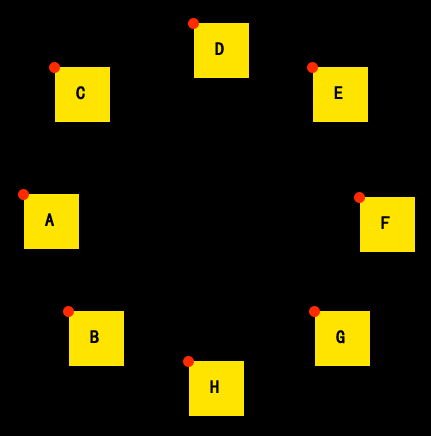
效果圖:
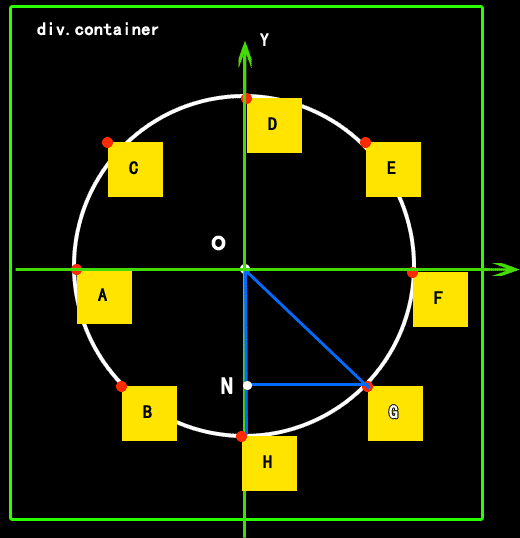
一、分析圖:
綠色邊框內:外層的DIV元素,相對定位;
白色圓形框:輔助分析的想象形狀;
白點:為白色圓形的圓心點,中心點,點o;
圓心角:角NOG;
黃色:需要按圓形排列的,絕對定位的DIV元素;
紅色點:為每個黃色DIV的坐標點;即絕對定位時的元素,left值 和 top值 ,設置的點;
二、涉及到的概念定義:
2.1、弧度:弧度是角的度量單位。
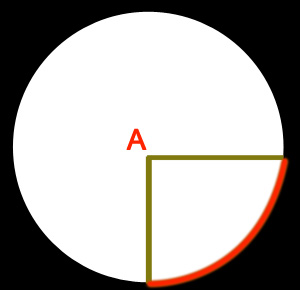
(紅色部分為弧長,角A為弧長對應的圓心角)
弧長等於半徑的弧,其所對的圓心角為1弧度。(即兩條射線從圓心向圓周射出,形成一個夾角和夾角正對的一段弧。當這段弧長正好等於圓的半徑時,兩條射線的夾角的弧度為1)。
根據定義,一周的弧度數為2πr/r=2π,360°角=2π弧度,因此,1弧度約為57.3°,即57°17'44.806'',1°為π/180弧度,近似值為0.01745弧度,周角為2π弧度,平角(即180°角)為π弧度,直角為π/2弧度。
弧長=n2πr/360 (在這裡n就是角度數,即圓心角n所對應的弧長。)
========================================================
2.2、正弦值:弦值是在直角三角形中,對邊的長比上斜邊的長的值。
Math.sin(x) : X 必需。一個以弧度表示的角。將角度乘以 0.017453293 (2PI/360)即可轉換為弧度。
================================================
2.3、余弦值:是指直角三角形銳角鄰邊與斜邊的比值。
Math.sin(x) : X 必需。一個以弧度表示的角。將角度乘以 0.017453293 (2PI/360)即可轉換為弧度。
三、需求分析:
3.1 讓這些黃色的DIV ,在同一個圓的圓周上排列
3.2 排列的方式是平均分布
四、原理分析:
要讓DIV的排列,形成一個圓形,實質就是設置每個DIV的left值 和 TOP值 之間的關系,讓它們之間值的關系,按照圓形的規律去設值;
4.1 圓形的規律是什麼?
是PI(圓周率); 任何值乘以這個PI再乘2,就可以得到一個圓形。這個“任何值”就是得到的圓形的半徑;值越大,當然這個圓形也就越大。
4.2 怎麼找到每個DIV的Left 和 TOP值之關系?
上圖中的每個黃色DIV左上角的紅色點的坐標,就是left 和 TOP值 ,要讓這個紅色的點,正好分布在這個圓周上面,那麼Left 和 top 必然要和這個PI關聯起來。有PI才有圓。
五、實例分析
我要得到上圖中,紅點的坐標值,即DIV的left 和 TOP值,
LEFT = NG + o的橫坐標值(left)
TOP = ON + or的縱坐標值(TOP)
所以先要求出每個一以圓心o為頂點,以圓形半徑為斜邊,的直角三角形的兩個直角邊的值。(上圖中藍色直角三角形的ON線段和NG線段的長度值)
以半邊圓形來看,當圓心角變大,半徑不變的情況下,這個底邊的值,是會變大的;
正弦公式:sin(X) = 對邊/斜邊 X變大,斜邊不變(半徑),那麼對邊(上圖中的NG線段)是會變大的;
余統公式 cos(X) = 鄰邊/斜邊 X變大,斜邊不變(半徑),那麼鄰邊(上圖中ON線段) 是會變小的;
270度的正統值,是負1;
180的余弦值是,是負1;
5.1 先設定一個圓
半徑:200px;
5.2 平均這個圓的圓周
假設我們有8個DIV 要平均分布在這個半徑為200PX的圓周上面。那麼這裡我們通過角度去平均(弧線的劃分也好,平均也好,冒似都應該通過角度去劃分);
平均:圓形的圓心角的總角度為360度,平均成8份,就是360/8; 這樣平分後的每一個圓心角,所對的弧長,弧度,就都是相等的。
5.3 求出NG的長度值,也就是DIV的left值,即紅點的橫坐標值;
求這個值,要用到正弦函數;
公式 Math.sin(X) = 對邊/斜邊;
我們需要知道X,需要知到斜邊;就可以求出“對邊”值,即NG的長度值;
5.3.1 這裡的X是弧度,即角度數;上面定義中說過,弧度數是表示角度數的;
根據公式: 角度數乘以 PI/180,就是弧度數; 即 X = (360/8)* PI/180
這個求出的X就是把圓形平分之後,的弧度數;
5.3.2 斜邊,就是這個圓形的半徑,即 200;
5.3.3 “對邊”值,即NG的長度值;
根據上面的公式變形:對邊(NG ) = Math.sin(X)*斜邊
即 :對邊(NG )= Math.sin(X)* 200 = Math.sin( (360/8)* PI/180 )* 200;
好了,現在把對邊(NG )的值求出來了;也就是紅點的橫坐標值,即DVI的LEFT值;
5.4 求出每一個圓心角對應的直角邊,即對邊的長度值
因為每一個圓心角,都是均分的,所以乘以一個倍數,就得到不周圓心角對應的弧度值,即角度值
這裡用DIV的索引為倍數,值乘以X,就得到每個均分後,每個圓心角的弧度值;
對邊 = Math.sin(X*索引)* 200;
用這個求出的【對邊】值 做為DIV的left值;
5.5 DIV的TOP值,即ON線段的長度值
以上面四點的原理一樣,只不過把正弦值,改為余弦值
鄰邊(ON) = Math.COS(X*索引)* 200;
把這個值設為 DIV的TOP值;
根據以上分析:代碼如下,就可以按一個圓形,來排列DIV
//半徑
var radius = 200;
//每一個BOX對應的角度;
var avd = 360/$(".box").length;
//每一個BOX對應的弧度;
var ahd = avd*Math.PI/180;
$(".box").each(function(index, element){
$(this).css({"left":Math.sin((ahd*index))*radius,"top":Math.cos((ahd*index))*radius});
});
5.6 設置這個圓形的位置
圓形的位置,是根據這個圓形的圓心坐標來定的,所以我們就是要設置,圓心的坐標值,left top
圓心的坐標坐變化了,那麼對應DIV的left top也應該改變;
比如圓心的left :100PX ; TOP:100px;
那麼每個DIV的LEFT和TOP也應該加上這個值:
代碼如下
$(function(){
//中心點橫坐標
var dotLeft = ($(".container").width()-$(".dot").width())/2;
//中心點縱坐標
var dotTop = ($(".container").height()-$(".dot").height())/2;
//起始角度
var stard = 0;
//半徑
var radius = 200;
//每一個BOX對應的角度;
var avd = 360/$(".box").length;
//每一個BOX對應的弧度;
var ahd = avd*Math.PI/180;
//設置圓的中心點的位置
$(".dot").css({"left":dotLeft,"top":dotTop});
$(".box").each(function(index, element){
$(this).css({"left":Math.sin((ahd*index))*radius+dotLeft,"top":Math.cos((ahd*index))*radius+dotTop});
});
})
六 總結:
6.1 在涉及到曲線或弧線的時候,應該用角度或弧度去分析,找關聯;
6.2 找關系或比例,讓值和值之間是一個關系式,會用到乘以或除以一個倍數;( 例如以前寫過的放大鏡,就是用比例關系);
七 先前的理解有誤,現在更新了分析的圖片和分析;感謝 “ 弦”!的提示~
以上就是本文的全部內容,希望對大家有所幫助,有興趣的朋友可以看下《基於javascript實現按圓形排列DIV元素(二)》和《基於javascript實現按圓形排列DIV元素(三)》,謝謝對的支持!