在論壇和聊天室這樣的場景裡,為了保證用戶體驗,我們經常需要屏蔽很多不良詞語。對於單個關鍵詞查找,自然是indexOf、正則那樣的方式效率比較高。但對於關鍵詞較多的情況下,多次重復調用indexOf、正則的話去匹配全文的話,性能消耗非常大。由於目標字符串通常來說體積都比較大,所以必須要保證一次遍歷就得到結果。根據這樣的需求,很容易就想到對全文每個字符依次匹配的方式。比如對於這段文字:“Mike Jordan had said "Just do IT", so Mark has been a coder.”,假如我們的關鍵詞是“Mike”“Mark”,那麼可以遍歷整句話,當找到“M”就接著看能不能匹配到“i”或者“a”,能一直匹配到最後則成功找到一個關鍵詞,否則繼續遍歷。那麼關鍵詞的結構就應該是這樣的:
var keywords = {
M: {
i: {
k: {
e: {end: true}
}
},
a: {
r: {
k: {end: true}
}
}
}
}
由上文可以看出這個數據就是一個樹結構,而根據關鍵詞組來創建樹結構還是比較耗時的,而關鍵詞卻又是我們早已給定的,所以可以在匹配前預先創建這樣的數據結構。代碼如下:
function buildTree(keywords) {
var tblCur = {},
key, str_key, Length, j, i;
var tblRoot = tblCur;
for(j = keywords.length - 1; j >= 0; j -= 1) {
str_key = keywords[j];
Length = str_key.length;
for(i = 0; i < Length; i += 1) {
key = str_key.charAt(i);
if(tblCur.hasOwnProperty(key)) {
tblCur = tblCur[key];
} else {
tblCur = tblCur[key] = {};
}
}
tblCur.end = true; //最後一個關鍵字
tblCur = tblRoot;
}
return tblRoot;
}
這段代碼中用了一個連等語句:tblCur = tblCur[key] = {},這裡要注意的是語句的執行順序,由於[]的運算級比=高,所以首先是在 tblCur對象中先創建一個key屬性。結合tblRoot = tblCur = {} 看,執行順序就是:
var tblRoot = tblCur = {};
tblRoot = tblCur;
tblCur['key'] = undefined; // now tblRoot = {key: undefined}
tblCur['key'] = {};
tblCur = tblCur['key'];
通過上面的代碼就構建了好了所需的查詢數據,下面看看查詢接口的寫法。
對於目標字符串的每一字,我們都從這個keywords頂部開始匹配。首先是 keywords[a] ,若存在,則看 keyword[a][b],若最後 keyword[a][b]…[x]=true 則說明匹配成功,若 keyword[a][b]…[x]=undefined,則從下一個位置重新開始匹配 keywords[a] 。
function search(content) {
var tblCur,
p_star = 0,
n = content.length,
p_end,
match, //是否找到匹配
match_key,
match_str,
arrMatch = [], //存儲結果
arrLength = 0; //arrMatch的長度索引
while(p_star < n) {
tblCur = tblRoot; //回溯至根部
p_end = p_star;
match_str = "";
match = false;
do {
match_key = content.charAt(p_end);
if(!(tblCur = tblCur[match_key])) { //本次匹配結束
p_star += 1;
break;
} else {
match_str += match_key;
}
p_end += 1;
if(tblCur.end) //是否匹配到尾部
{
match = true;
}
} while (true);
if(match) { //最大匹配
arrMatch[arrLength] = {
key: match_str,
begin: p_star - 1,
end: p_end
};
arrLength += 1;
p_star = p_end;
}
}
return arrMatch;
}
以上就是整個關鍵詞匹配系統的核心。這裡很好的用到了js的語言特性,效率非常高。我用一篇50萬字的《搜神記》來做測試,從中查找給定的300個成語,匹配的效果是1秒左右。重要的是,由於目標文本是一次遍歷的,所以目標文本的長短對查詢時間的影響幾乎不計。對查詢時間影響較大的是關鍵詞的數量,目標文本的每個字都遍歷一遍關鍵詞,所以對查詢有一定影響。
簡單分析
看到上文估計你也納悶,對每個字都遍歷一遍所有關鍵詞,就算有些關鍵詞有部分相同,但是完全遍歷也是挺耗時的呀。但js中對象的屬性是使用哈希表來進行構建的,這種結構的數據跟單純的數組遍歷是有很大不同的,效率要比基於順序的數組遍歷高得多。可能有些同學對數據結構不太熟悉,這裡我簡單說一下哈希表的相關內容。
首先看看數據的存儲。
數據在內存的存儲由兩部分組成,一部分是值,另一部分是地址。把內存想象成一本新華字典,那字的解釋就是值,而目錄就是地址。字典裡面是按拼音排序的,比如相同發音的“ni”就排在同一塊,也就是說數組整齊排列在一塊內存區域裡面,這樣的結構就是數組,你可以指定“ni” 1號,10號來訪問。結構圖如下:

數組的優勢是遍歷簡單,通過下標就能直接訪問相應的數據了。但是它要增刪某一項就非常困難。比如你要把第6項刪掉,那第5項之後的數據都要向前移一個位置。如果你要刪除第一位,整個數組都要移動,消耗非常大。
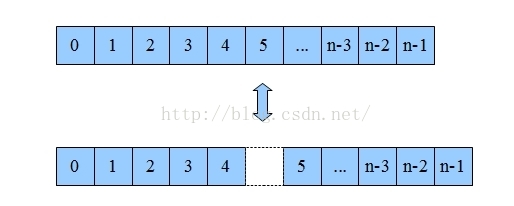
為了解決數組增刪的問題,鏈表就出現了。如果我們將值分成兩部分,一部分用來儲存原來的值,另一部分用來儲存一個地址,這個地址指向另外一個同樣的結構,以此類推就構成了一個鏈表。結構如下:

從上圖可以明顯看出,對鏈表進行增刪非常簡單,只要把目標項和前一項的next改寫就完成了。但是要查詢某個項的值就非常困難了,你必須依次遍歷才可以訪問到目標位置。
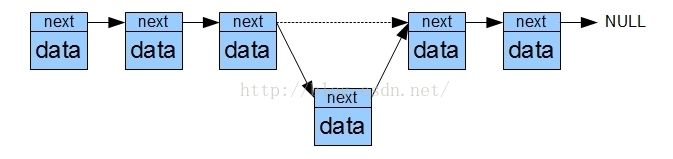
為了整合這兩種結構的優勢,聰明如你一定想到了下面這種結構。
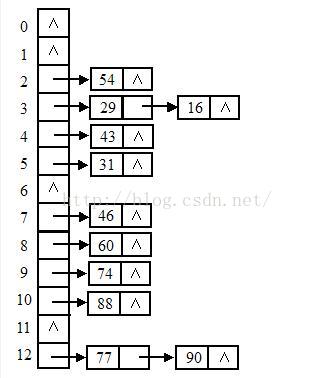
這種數據結構就是哈希表結構。數組裡面存儲鏈表的頭地址,就可以形成一個二維數據表。至於數據如何分布,這個就是哈希算法,正規的翻譯應該是散列算法。算法雖然有很多種,原理上都是通過一個函數對key進行求解,再根據求解得到的結果安放數據。也就是說key和實際地址之間形成了一個映射,所以這個時候我們不再以數組下標或者單純的遍歷來訪問數組,而是以散列函數的反函數來定位數據。js中的對象就是一個哈希結構,比如我們定義一個obj,obj.name通過散列,他在內存中的位置可能是上圖中的90,那我們想要操作obj.name的時候,底層就會自動幫我們通過哈希算法定位到90的位置,也就是說直接從數組的12項開始查找鏈表,而不是從0開始遍歷整個內存塊。
js中定義一個對象obj{key: value},key是被轉換成字符串然後經過哈希處理得到一個內存地址,然後將值放入其中。這就可以理解為什麼我們可以隨意增刪屬性,也能理解為什麼在js中還能為數組賦屬性,而且數組也沒有所謂的越界了。
在數據量較大的場合,哈希表具有非常明顯的優勢,因為它通過哈希算法減少了很多不必要的計算。所謂性能優化,其實就是讓計算機少運算;最大的優化,就是不計算!
算法的優化
現在理解算法底層實現,回過頭來就可以考慮對算法進行優化了。不過在優化前還是要強調一句:不要盲目追求性能!比如本案例中,我們最多就是5000字的匹配,那現有算法足矣,所有優化都是不必要的。之所以還來說說優化,就是為了提高自己對算法對程序的理解,而不是真的要去做那1ms的優化。
我們發現我們的關鍵詞都沒有一個字的,那我們按照一個字的單位進行關鍵詞遍歷顯然就是一個浪費了。這裡的優化就是預先統計關鍵詞的最大最小長度,每次以最小長度為單位進行查找。比如說我測試用例的關鍵詞是成語,最短都是4個字,那麼我每次匹配都是4個字一起匹配,如果命中就繼續深入查找到最大長度。也就是說我們最開始構造樹的時候首先是以最小長度構建的,然後再逐字增加。
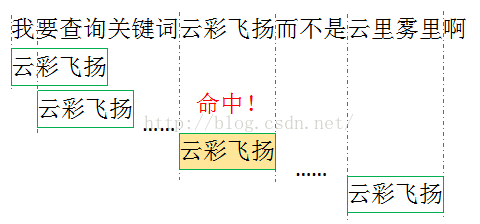
簡單計算一下,按照我們的測試用例,300個成語,我們匹配一個詞只需一次對比,而單字查詢的話我們需要對比4次,而每次對比我們都要訪問我們的樹結構,這就是可避免的性能消耗。更重要的是,這裡的對比並不是字符串對比,這裡我們的關鍵字都是作為key存在的,效果就是 和key in obj一樣的,都是對key進行哈希變換然後訪問相應的地址!所以千萬不要糾結對比一個字和對比4個字的差異,我們沒對比字符串!
關於多關鍵詞的匹配就說到這裡了,優化版代碼我就不貼了,因為一般也用不到。