我們可以看到在javascript概念中的隊列與棧都是一種特殊的線性表的結構,也是一種比較簡單的基於數組的順序存儲結構。由於javascript的解釋器針對數組都做了直接的優化,不會存在在很多編程語言中數組固定長度的問題(當數組填滿後再添加就比較困難了,包括添加刪除,都是需要把數組中所有的元素全部都變換位置的,javascript的的數組確實直接給優化好了,如push,pop,shift,unshift,split方法等等…)
線性表的順序存儲結構,最大的缺點就是改變其中一個元素的排列時都會引起整個合集的變化,其原因就是在內存中的存儲本來就是連貫沒有間隙的,刪除一個自然就要補上。針對這種結構的優化之後就出現了鏈式存儲結構,換個思路,我們完全不關心數據的排列,我們只需要在每一個元素的內部把下一個的數據的位置給記錄就可以了,所以用鏈接方式存儲的線性表簡稱為鏈表,在鏈式結構中,數據=(信息+地址)
鏈式結構中,我們把地址也可以稱為“鏈”,一個數據單元就是一個節點,那麼可以說鏈表就是一組節點組成的合集。每一個節點都有一個數據塊引用指向它的下一個節點
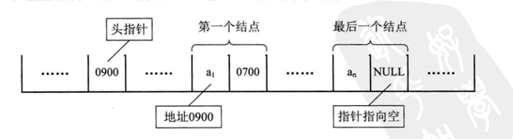
數組元素是靠位置關系做邏輯引用,鏈表則是靠每一個數據元保存引用指針關系進行引用
這種結構上的優勢就非常明顯的,插入一個數據完全不需要關心其排列情況,只要把“鏈”的指向銜接上
這樣做鏈表的思路就不會局限在數組上了,我們可以用對象了,只要對象之間存在引用關系即可
鏈表一般有,單鏈表、靜態鏈表、循環鏈表、雙向鏈表
單鏈表:就是很單一的向下傳遞,每一個節點只記錄下一個節點的信息,就跟無間道中的梁朝偉一樣做臥底都是通過中間人上線與下線聯系,一旦中間人斷了,那麼就無法證明自己的身份了,所以片尾有一句話:"我是好人,誰知道呢?”
靜態鏈表:就是用數組描述的鏈表。也就是數組中每一個下表都是一個“節”包含了數據與指向
循環鏈表:由於單鏈表的只會往後方傳遞,所以到達尾部的時候,要回溯到首部會非常麻煩,所以把尾部節的鏈與頭連接起來形成循環
雙向鏈表:針對單鏈表的優化,讓每一個節都能知道前後是誰,所以除了後指針域還會存在一個前指針域,這樣提高了查找的效率,不過帶來了一些在設計上的復雜度,總體來說就是空間換時間了
綜合下,其實鏈表就是線性表中針對順序存儲結構的一種優化手段,但是在javascript語言中由於數組的特殊性(自動更新引用位置),所以我們可以采用對象的方式做鏈表存儲的結構
單鏈表
我們實現一個最簡單的鏈表關系
function createLinkList() {
var _this = {},
prev = null;
return {
add: function(val) {
//保存當前的引用
prev = {
data: val,
next: prev || null
}
}
}
}
var linksList = createLinkList();
linksList.add("arron1");
linksList.add("arron2");
linksList.add("arron3");
//node節的next鏈就是 -arron3-arron2-arron1
通過node對象的next去直引用下一個node對象,初步是實現了通過鏈表的引用,這種鏈式思路jQuery的異步deferred中的then方法,還有日本的cho45的jsderferre中都有用到。這個實現上還有一個最關鍵的問題,我們怎麼動態插入數據到執行的節之後?
所以我們必須 要設計一個遍歷的方法,用來搜索這個node鏈上的數據,然後找出這個對應的數據把新的節插入到當前的鏈中,並改寫位置記錄
//在鏈表中找到對應的節
var findNode = function createFindNode(currNode) {
return function(key){
//循環找到執行的節,如果沒有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
這就是一個查找當前節的一個方法,通過傳遞原始的頭部headNode節去一直往下查找next,直到找到對應的節信息
這裡是用curry方法實現的
那麼插入節的的時候,針對鏈表地址的換算關系這是這樣
a-b-c-d的鏈表中,如果要在c(c.next->d)後面插入一個f
a-b-c-f-d ,那麼c,next->f , f.next-d
通過insert方法增加節
//創建節
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化頭部節
//從headNode開始形成一條鏈條
//通過next銜接
var headNode = new createNode("head");
//在鏈表中找到對應的節
var findNode = function createFindNode(currNode) {
return function(key){
//循環找到執行的節,如果沒有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一個新節
this.insert = function(data, key) {
//創建一個新節
var newNode = new createNode(data);
//在鏈條中找到對應的數據節
//然後把新加入的掛進去
var current = findNode(key);
//插入新的接,更改引用關系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
首先分離出createNode節的構建,在初始化的時候先創建一個頭部節對象用來做節開頭的初始化對象
在insert增加節方法中,通過對headNode鏈的一個查找,找到對應的節,把新的節給加後之後,最後就是修改一下鏈的關系
如何從鏈表中刪除一個節點?
由於鏈表的特殊性,我們a->b->c->d ,如果要刪除c那麼就必須修改b.next->c為 b.next->d,所以找到前一個節修改其鏈表next地址,這個有點像dom操作中removeChild找到其父節點調用移除子節點
同樣的我們也在remove方法的設計中,需要設計一個遍歷往上回溯一個父節點即可
//找到前一個節
var findPrevious = function(currNode) {
return function(key){
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改鏈表關系
prevNode.next = prevNode.next.next;
}
};
測試代碼:
<!doctype html><button id="test1">插入多條數據</button>
<button id="test2">刪除Russellville數據</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//創建鏈表 //
//////////
function createLinkList() {
//創建節
function createNode(data) {
this.data = data;
this.next = null;
}
//初始化頭部節
//從headNode開始形成一條鏈條
//通過next銜接
var headNode = new createNode("head");
//在鏈表中找到對應的節
var findNode = function createFindNode(currNode) {
return function(key) {
//循環找到執行的節,如果沒有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//找到前一個節
var findPrevious = function(currNode) {
return function(key) {
while (!(currNode.next == null) &&
(currNode.next.data != key)) {
currNode = currNode.next;
}
return currNode;
}
}(headNode);
//插入一個新節
this.insert = function(data, key) {
//創建一個新節
var newNode = new createNode(data);
//在鏈條中找到對應的數據節
//然後把新加入的掛進去
var current = findNode(key);
//插入新的接,更改引用關系
//1:a-b-c-d
//2:a-b-n-c-d
newNode.next = current.next;
current.next = newNode;
};
//插入方法
this.remove = function(key) {
var prevNode = findPrevious(key);
if (!(prevNode.next == null)) {
//修改鏈表關系
prevNode.next = prevNode.next.next;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>
雙鏈表
原理跟單鏈表是一樣的,無非就是給每一個節增加一個前鏈表的指針
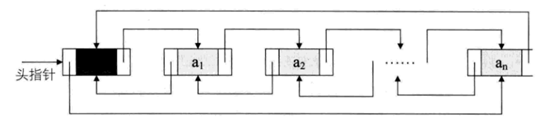
增加節
//插入一個新節
this.insert = function(data, key) {
//創建一個新節
var newNode = new createNode(data);
//在鏈條中找到對應的數據節
//然後把新加入的掛進去
var current = findNode(headNode,key);
//插入新的接,更改引用關系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
刪除節
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};
在刪除操作中有一個明顯的優化:不需要找到父節了,因為雙鏈表的雙向引用所以效率比單鏈要高
測試代碼:
<!doctype html><button id="test1">插入多條數據</button>
<button id="test2">刪除Russellville數據</button><div id="listshow"><br /></div><script type="text/javascript">
//////////
//創建鏈表 //
//////////
function createLinkList() {
//創建節
function createNode(data) {
this.data = data;
this.next = null;
this.previous = null
}
//初始化頭部節
//從headNode開始形成一條鏈條
//通過next銜接
var headNode = new createNode("head");
//在鏈表中找到對應的數據
var findNode = function(currNode, key) {
//循環找到執行的節,如果沒有返回本身
while (currNode.data != key) {
currNode = currNode.next;
}
return currNode;
}
//插入一個新節
this.insert = function(data, key) {
//創建一個新節
var newNode = new createNode(data);
//在鏈條中找到對應的數據節
//然後把新加入的掛進去
var current = findNode(headNode,key);
//插入新的接,更改引用關系
newNode.next = current.next;
newNode.previous = current
current.next = newNode;
};
this.remove = function(key) {
var currNode = findNode(headNode,key);
if (!(currNode.next == null)) {
currNode.previous.next = currNode.next;
currNode.next.previous = currNode.previous;
currNode.next = null;
currNode.previous = null;
}
};
this.display = function(fn) {
var currNode = headNode;
while (!(currNode.next == null)) {
currNode = currNode.next;
fn(currNode.data)
}
};
}
var cities = new createLinkList();
function create() {
var text = '';
cities.display(function(data) {
text += '-' + data;
});
var div = document.createElement('div')
div.innerHTML = text;
document.getElementById("listshow").appendChild(div)
}
document.getElementById("test1").onclick = function() {
cities.insert("Conway", "head");
cities.insert("Russellville", "Conway");
cities.insert("Carlisle", "Russellville");
cities.insert("Alma", "Carlisle");
create();
}
document.getElementById("test2").onclick = function() {
cities.remove("Russellville");
create()
}
</script>
git代碼下載:https://github.com/JsAaron/data_structure.git