開學一個月,已經多次夢見筆試出現數據結構算法題,我對數據結構的恐懼已經多於任何“妖魔鬼怪”了。呵呵,看來真的很有必要復習一下常用的數據結構,免得“噩夢”成真。
數據機構等編程基礎的重要性不用多說,直接進入正題。
排序算法,分為內部排序和外部排序。內部排序要使用內存,這裡只探討內部排序。
1,插入排序:直接插入排序和希爾排序
2,選擇排序:簡單選擇排序和堆排序
3,交換排序:冒泡排序和快速排序
4,歸並排序
5,基數排序

直接插入排序
基本思想:在要排序的一組數,假設前面(n-1)[n>=2]個數已經是排好順序的,先要把第n個數插入到前面的有序數,使得這n個數也是排好順序的。如此反復循環,知道全部排好順序。
希爾排序
基本思想:算法先將要排序的一組數按某個增量d(n/2,n為要排序的個數)分成若干組,每組中記錄的下標相差d。對每組中全部元素進行直接插入排序,然後再用一個較小的增量(d/2)對它進行分組,在每組中再進行直接插入排序。當增量減到1時,進行直接插入排序後,排序完成。
簡單選擇排序
基本思想:在要排序的一組數中,選出最小的一個數與第一個位置的數交換,然後剩下的數當中找出最小的與第二個位置的數交換,如此尋哈un到倒數第二個數和最後一個數為止。
堆排序
基本思想:堆排序是一種樹形選擇排序,是對直接選擇排序的有效改進。
具有n個元素的序列(h1,h2,...,hn),當且僅當滿足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,...,n/2)時稱之為堆。在這裡只討論滿足前者條件的堆。由堆的定義可以看出,堆頂元素(即第一個元素)必為最大項(大頂堆)。完全二叉樹可以很直觀地表示堆的結構。堆頂為根,其它為左子樹、右子樹。初始時把要排序的數的序列看作是一棵順序存儲的二叉樹,調整它們的存儲序,使之成為一個堆,這時堆的根節點的數最大。然後將根節點與堆的最後一個節點交換。然後對前面(n-1)個數重新調整使之成為堆。依此類推,直到只有兩個節點的堆,並對它們作交換,最後得到有n個節點的有序序列。從算法描述來看,堆排序需要兩個過程,一是建立堆,二是堆頂與堆的最後一個元素交換位置。所以堆排序有兩個函數組成。一是建堆的滲透函數,二是反復調用滲透函數實現排序的函數。
冒泡排序
基本思想:在要排序的一組數中,對當前還未排好序的范圍內的全部數,自上而下對相鄰的兩個數依次進行比較和調整,讓較大的數往下沉,較小的往上冒。即:每當兩相鄰的數比較後發現它們的排序與排序要求相反時,就將它們互換。
快速排序
基本思想:選擇一個基准元素,通常選擇第一個元素或者最後一個元素,通過一趟掃描,將待排序列分成兩部分,一部分比基准元素小,一部分大於等於基准元素,此時基准元素在其排好序後的正確位置,然後再用同樣的方法遞歸地排序劃分的兩部分。
歸並排序
基本排序:歸並(Merge)排序法是將兩個(或兩個以上)有序表合並成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合並為整體有序序列。
基數排序
基本思想:將所有待比較數值(正整數)統一為同樣的數位長度,數位較短的數前面補零。然後,從最低位開始,依次進行一次排序。這樣從最低位排序一直到最高位排序完成以後,數列就變成一個有序序列。
代碼演示地址:http://lovermap.sinaapp.com/test/sort.html
現在我們分析一下8種排序算法的穩定性。
(請網友結合前面的排序基本思想來理解排序的穩定性(8種排序的基本思想已經在前面說過,這裡不再贅述)不然可能有些模糊)
(1)直接插入排序:一般插入排序,比較是從有序序列的最後一個元素開始,如果比它大則直接插入在其後面,否則一直往前比。如果找到一個和插入元素相等的,那麼就插入到這個相等元素的後面。插入排序是穩定的。
(2)希爾排序:希爾排序是按照不同步長對元素進行插入排序,一次插入排序是穩定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,穩定性就會被破壞,所以希爾排序不穩定。
(3)簡單選擇排序:在一趟選擇,如果當前元素比一個元素小,而該小的元素又出現在一個和當前元素相等的元素後面,那麼交換後穩定性就被破壞了。光說可能有點模糊,來看個小實例:858410,第一遍掃描,第1個元素8會和4交換,那麼原序列中2個8的相對前後順序和原序列不一致了,所以選擇排序不穩定。
(4)堆排序:堆排序的過程是從第n/2開始和其子節點共3個值選擇最大(大頂堆)或者最小(小頂堆),這3個元素之間的選擇當然不會破壞穩定性。但當為n/2-1, n/2-2, ...這些父節點選擇元素時,有可能第n/2個父節點交換把後面一個元素交換過去了,而第n/2-1個父節點把後面一個相同的元素沒有交換,所以堆排序並不穩定。
(5)冒泡排序:由前面的內容可知,冒泡排序是相鄰的兩個元素比較,交換也發生在這兩個元素之間,如果兩個元素相等,不用交換。所以冒泡排序穩定。
(6)快速排序:在中樞元素和序列中一個元素交換的時候,很有可能把前面的元素的穩定性打亂。還是看一個小實例:6 4 4 5 4 7 8 9,第一趟排序,中樞元素6和第三個4交換就會把元素4的原序列破壞,所以快速排序不穩定。
(7)歸並排序:在分解的子列中,有1個或2個元素時,1個元素不會交換,2個元素如果大小相等也不會交換。在序列合並的過程中,如果兩個當前元素相等時,我們把處在前面的序列的元素保存在結果序列的前面,所以,歸並排序也是穩定的。
(8)基數排序:是按照低位先排序,然後收集;再按照高位排序,然後再收集;依次類推,直到最高位。有時候有些屬性是有優先級順序的,先按低優先級排序,再按高優先級排序,最後的次序就是高優先級高的在前,高優先級相同的低優先級高的在前。基數排序基於分別排序,分別收集,所以是穩定的。
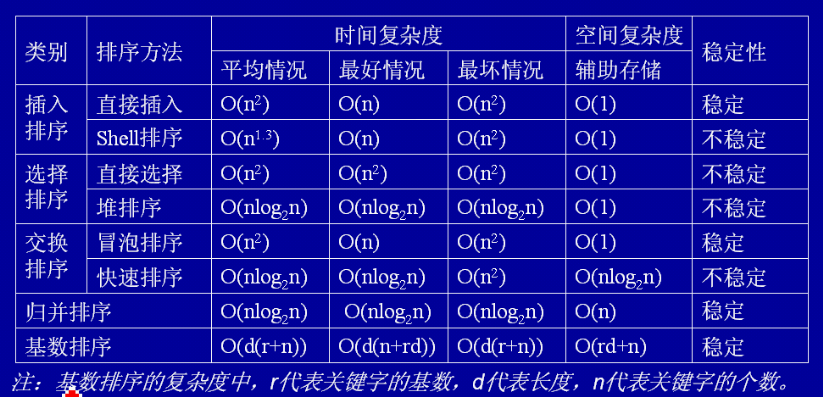
8種排序的分類,穩定性,時間復雜度和空間復雜度總結:
以上所述就是本文的全部內容了,希望大家能夠喜歡。