在前面一文,說過二叉樹的遞歸遍歷算法(二叉樹先根(先序)遍歷的改進),此文主要講二叉樹的非遞歸算法,采用棧結構
總結先根遍歷得到的非遞歸算法思想如下:
1)入棧,主要是先頭結點入棧,然後visit此結點
2)while,循環遍歷當前結點,直至左孩子沒有結點
3)if結點的右孩子為真,轉入1)繼續遍歷,否則退出當前結點轉入父母結點遍歷轉入1)
先看符合此思想的算法:
復制代碼 代碼如下:
int PreOrderTraverseNonRecursiveEx(const BiTree &T, int (*VisitNode)(TElemType data))
{
if (T == NULL)
{
return -1;
}
BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
while (!IsStackEmpty(S))
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}
pBiNode = pBiNode->lchild;
}
if(pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode);
}
if ( pBiNode->rchild == NULL)
{
Pop(&S, (SElemType*)&pBiNode); //如果此時棧已空,就有問題
}
pBiNode = pBiNode->rchild;
}
return 0;
}
注意:1)這裡使用了棧結構,可參看上文順序結構存儲的棧
2)這裡在保存結點的時候,我保存的是指針也就是結點的地址,將其變為int型存儲,在pop的時候裡面使用的是指針,所以取的是&pBiNode,而不是pBiNode,為什麼請自行思考指針的使用,最好理解的就是BiTNode *pBiNode;定義改為BiTree pBiNode就很好理解了。
上面這個算法其實是錯誤的!為什麼呢? 這裡我檢查好久,期間出現還出現過無限循環,也出現過從左子樹退出後右邊子樹不顯示,最後我修改了第一個while判斷條件,為什麼呢?因為如果在pop之後,棧已空但是右子樹還有,就無法繼續了,這個在我寫出後並沒有進行太多驗證,後面再闡述,這裡並沒有壓入null指針,看一下壓入空指針的例子,主要是左子樹為空的時候才壓入棧的,如下:
復制代碼 代碼如下:
int PreOrderTraverseNonRecursive(const BiTree &T, int (*VisitNode)(TElemType data))
{
if (T == NULL)
{
return -1;
}
BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
while (!IsStackEmpty(S))
{
GetTop(S, (SElemType*)&pBiNode);
while (pBiNode)
{
VisitNode(pBiNode->data);
pBiNode = pBiNode->lchild;
Push(&S, (SElemType)pBiNode);
}
if(pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode);
}
if ( !IsStackEmpty(S))
{
Pop(&S, (SElemType*)&pBiNode);
pBiNode = pBiNode->rchild;
Push(&S, (SElemType)pBiNode);
}
}
return 0;
}
這裡是這樣的,先壓入根節點,然後判斷左子樹是否為空,不為空就壓入棧,否則退出while循環之後就將NULL結點出棧,再判斷當前棧是否為空,如果非空就出棧得到父節點然後判斷右孩子,壓入右孩子結點,再判斷此右子樹的左孩子是否為空,繼續循環。
這裡有兩個浪費的地方:一個就是壓入空孩子結點入棧,二就是頻繁使用GetTop獲得棧頂元素
這裡返回過來再看初開始設計的算法,那裡正好沒有壓入NULL指針或者說空的孩子結點,但是並不能輸出完整,這裡我們想到可以在判斷棧的時候加入,當前的結點是否為NULL就可以了,這樣就不會出現不會顯示退出左子樹結點不能顯示右子樹結點的尴尬了,如下:
復制代碼 代碼如下:
//非遞歸先序遍歷二叉樹
int PreOrderTraverseNonRecursiveEx(const BiTree &T,
int (*VisitNode)(TElemType data))
{
if (T == NULL)
{
return -1;
}
BiTNode *pBiNode = T;
SqStack S;
InitStack(&S);
Push(&S, (SElemType)T);
while ( !IsStackEmpty(S) || pBiNode) //主要修改的就是這句
{
while (pBiNode)
{
VisitNode(pBiNode->data);
if (pBiNode != T)
{
Push(&S, (SElemType)pBiNode);
}
pBiNode = pBiNode->lchild;
}
if(pBiNode == NULL)
{
Pop(&S, (SElemType*)&pBiNode);
}
if ( pBiNode->rchild == NULL)
{
Pop(&S, (SElemType*)&pBiNode); //如果此時棧已空,就有問題
}
pBiNode = pBiNode->rchild;
}
return 0;
}
在第一個while循環加入這個之後,就可以了,測試用例與二叉樹先序遍歷類似。如下測試上節的二叉樹例子:
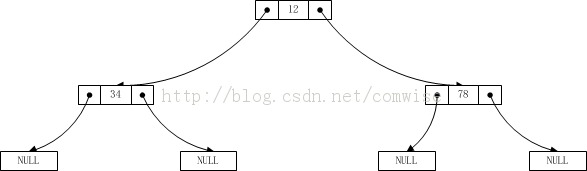
此時輸入的數據仍然還是 12 34 0 0 78 0 0,測試結果如下:
--- BiTree ---
Please Enter BiTree Node data:
12
Please Enter BiTree Node data:
34
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
78
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
12 34 78
這個還不足以測試,再看如下的二叉樹
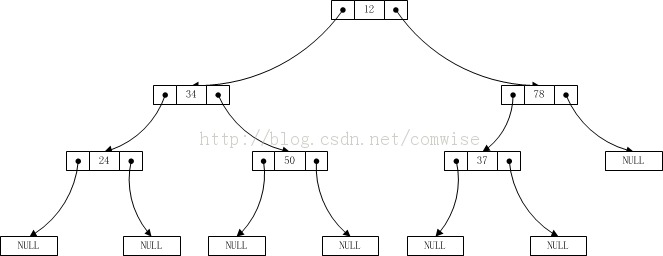
此時輸入數據應該為:12 34 24 0 0 50 0 0 78 37 0 0 0,測試結果如下:
--- BiTree ---
Please Enter BiTree Node data:
12
Please Enter BiTree Node data:
34
Please Enter BiTree Node data:
24
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
50
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
78
Please Enter BiTree Node data:
37
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
12 34 24 50 78 37
由先序遍歷可知,正好是正確的,另外這些算法不光是對先序遍歷的,如果想變為中序或者後序,只需將上面算法中的visit之類的先去掉,然後將它加入合適的位置,就可以了