二叉樹的概念
二叉樹(Binary Tree)是n(n>=0)個結點的有限集合,該集合或者為空集(空二叉樹),或者由一個根結點和兩棵互不相交的、分別稱為根結點的左子樹和右子樹的二叉樹組成。
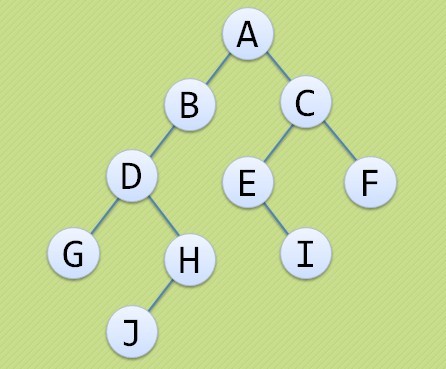
二叉樹的特點
每個結點最多有兩棵子樹,所以二叉樹中不存在度大於2的結點。二叉樹中每一個節點都是一個對象,每一個數據節點都有三個指針,分別是指向父母、左孩子和右孩子的指針。每一個節點都是通過指針相互連接的。相連指針的關系都是父子關系。
二叉樹節點的定義
二叉樹節點定義如下:
復制代碼 代碼如下:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
二叉樹的五種基本形態
空二叉樹
只有一個根結點
根結點只有左子樹
根結點只有右子樹
根結點既有左子樹又有右子樹
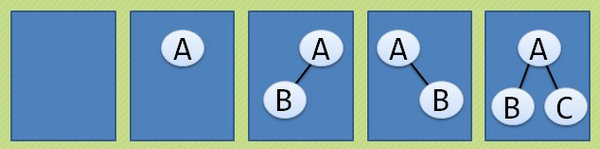
擁有三個結點的普通樹只有兩種情況:兩層或者三層。但由於二叉樹要區分左右,所以就會演變成如下的五種形態:
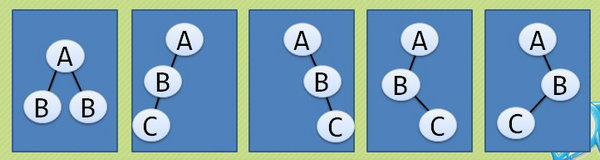
特殊二叉樹
斜樹
如上面倒數第一副圖的第2、3小圖所示。
滿二叉樹
在一棵二叉樹中,如果所有分支結點都存在左子樹和右子樹,並且所有葉子都在同一層上,這樣的二叉樹稱為滿二叉樹。如下圖所示:
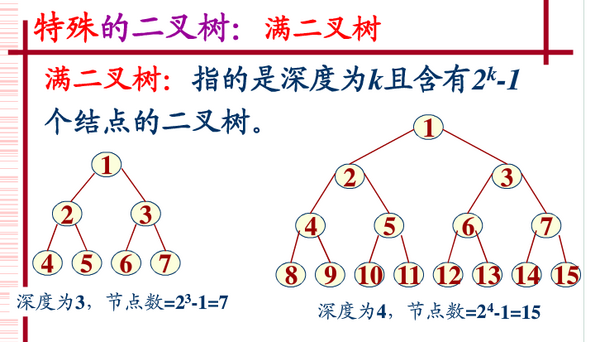
完全二叉樹
完全二叉樹是指最後一層左邊是滿的,右邊可能滿也可能不滿,然後其余層都是滿的。一個深度為k,節點個數為 2^k - 1 的二叉樹為滿二叉樹(完全二叉樹)。就是一棵樹,深度為k,並且沒有空位。
完全二叉樹的特點有:
葉子結點只能出現在最下兩層。
最下層的葉子一定集中在左部連續位置。
倒數第二層,若有葉子結點,一定都在右部連續位置。
如果結點度為1,則該結點只有左孩子。
同樣結點樹的二叉樹,完全二叉樹的深度最小。
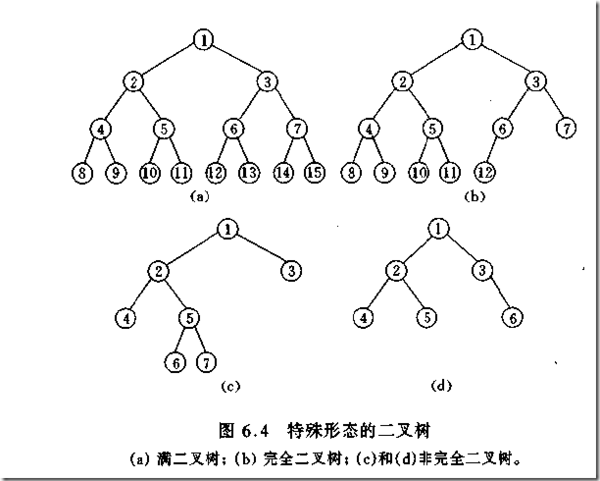
注意:滿二叉樹一定是完全二叉樹,但完全二叉樹不一定是滿二叉樹。
算法如下:
復制代碼 代碼如下:
bool is_complete(tree *root)
{
queue q;
tree *ptr;
// 進行廣度優先遍歷(層次遍歷),並把NULL節點也放入隊列
q.push(root);
while ((ptr = q.pop()) != NULL)
{
q.push(ptr->left);
q.push(ptr->right);
}
// 判斷是否還有未被訪問到的節點
while (!q.is_empty())
{
ptr = q.pop();
// 有未訪問到的的非NULL節點,則樹存在空洞,為非完全二叉樹
if (NULL != ptr)
{
return false;
}
}
return true;
}
二叉樹的性質
二叉樹的性質一:在二叉樹的第i層上至多有2^(i-1)個結點(i>=1)
二叉樹的性質二:深度為k的二叉樹至多有2^k-1個結點(k>=1)
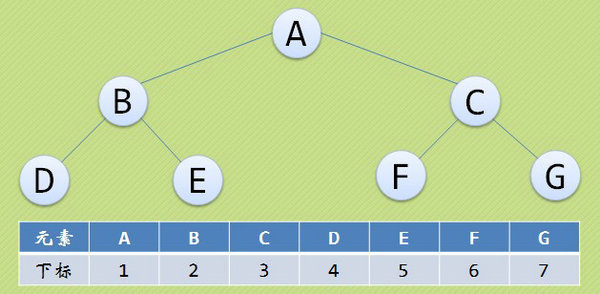
二叉樹的順序存儲結構
二叉樹的順序存儲結構就是用一維數組存儲二叉樹中的各個結點,並且結點的存儲位置能體現結點之間的邏輯關系。
二叉鏈表
既然順序存儲方式的適用性不強,那麼我們就要考慮鏈式存儲結構啦。二叉樹的存儲按照國際慣例來說一般也是采用鏈式存儲結構的。
二叉樹每個結點最多有兩個孩子,所以為它設計一個數據域和兩個指針域是比較自然的想法,我們稱這樣的鏈表叫做二叉鏈表。

二叉樹的遍歷
二叉樹的遍歷(traversing binary tree)是指從根結點出發,按照某種次序依次訪問二叉樹中所有結點,使得每個結點被訪問一次且僅被訪問一次。
二叉樹的遍歷有三種方式,如下:
(1)前序遍歷(DLR),首先訪問根結點,然後遍歷左子樹,最後遍歷右子樹。簡記根-左-右。
(2)中序遍歷(LDR),首先遍歷左子樹,然後訪問根結點,最後遍歷右子樹。簡記左-根-右。
(3)後序遍歷(LRD),首先遍歷左子樹,然後遍歷右子樹,最後訪問根結點。簡記左-右-根。
前序遍歷:
若二叉樹為空,則空操作返回,否則先訪問根結點,然後前序遍歷左子樹,再前序遍歷右子樹。
遍歷的順序為:A B D H I E J C F K G
復制代碼 代碼如下:
//先序遍歷
function preOrder(node){
if(!node == null){
putstr(node.show()+ " ");
preOrder(node.left);
preOrder(node.right);
}
}
中序遍歷:
若樹為空,則空操作返回,否則從根結點開始(注意並不是先訪問根結點),中序遍歷根結點的左子樹,然後是訪問根結點,最後中序遍歷右子樹。
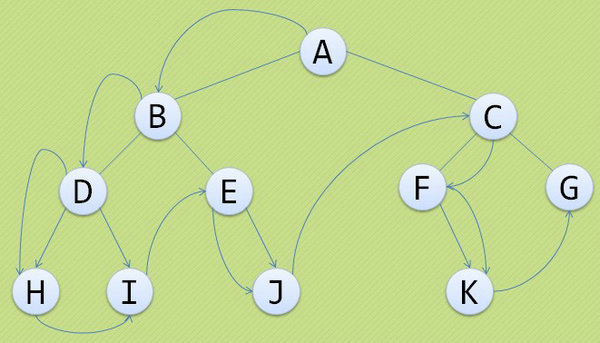
遍歷的順序為:H D I B E J A F K C G
復制代碼 代碼如下:
//使用遞歸方式實現中序遍歷
function inOrder(node){
if(!(node == null)){
inOrder(node.left);//先訪問左子樹
putstr(node.show()+ " ");//再訪問根節點
inOrder(node.right);//最後訪問右子樹
}
}
後序遍歷:
若樹為空,則空操作返回,否則從左到右先葉子後結點的方式遍歷訪問左右子樹,最後訪問根結點。
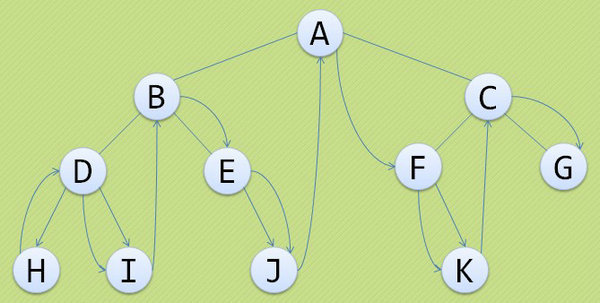
遍歷的順序為:H I D J E B K F G C A
復制代碼 代碼如下:
//後序遍歷
function postOrder(node){
if(!node == null){
postOrder(node.left);
postOrder(node.right);
putStr(node.show()+ " ");
}
}
實現二叉查找樹
二叉查找樹(BST)由節點組成,所以我們定義一個Node節點對象如下:
復制代碼 代碼如下:
function Node(data,left,right){
this.data = data;
this.left = left;//保存left節點鏈接
this.right = right;
this.show = show;
}
function show(){
return this.data;//顯示保存在節點中的數據
}
查找最大和最小值
查找BST上的最小值和最大值非常簡單,因為較小的值總是在左子節點上,在BST上查找最小值,只需遍歷左子樹,直到找到最後一個節點
查找最小值
復制代碼 代碼如下:
function getMin(){
var current = this.root;
while(!(current.left == null)){
current = current.left;
}
return current.data;
}
該方法沿著BST的左子樹挨個遍歷,直到遍歷到BST最左的節點,該節點被定義為:
復制代碼 代碼如下:
current.left = null;
這時,當前節點上保存的值就是最小值
查找最大值
在BST上查找最大值只需要遍歷右子樹,直到找到最後一個節點,該節點上保存的值就是最大值。
復制代碼 代碼如下:
function getMax(){
var current = this.root;
while(!(current.right == null)){
current = current.right;
}
return current.data;
}