圖的定義
圖(Graph)是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個圖,V是圖G中頂點的集合,E是圖G中邊的集合。
有向圖
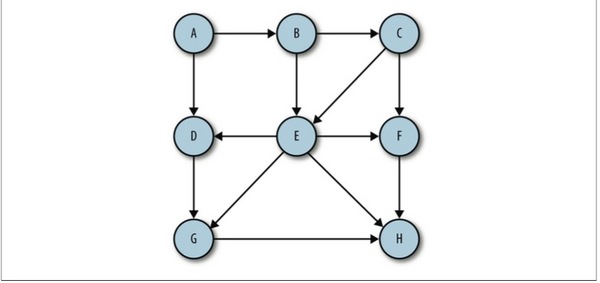
有向邊:若從頂點Vi到Vj的邊有方向,則稱這條邊為有向邊,也成為弧(Arc),用有序偶<Vi,Vj>來表示,Vi稱為弧尾,Vj稱為弧頭。
無序圖
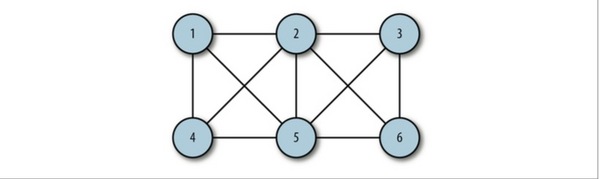
無向邊:若頂點Vi到Vj之間的邊沒有方向,則稱這條邊為無向邊(Edge),用無序偶(Vi,Vj)來表示。
簡單圖
簡單圖:在圖結構中,若不存在頂點到其自身的邊,且同一條邊不重復出現,則稱這樣的圖為簡單圖。
圖類
表示頂點
創建圖類的第一步就是要創建一個Vertex類來保存頂點和邊。這個類的作用和鏈表、二叉搜索樹的Node類一樣。Vertex類有兩個數據成員:一個用於標識頂點,另一個表明是否被訪問過的布爾值。分別被命名為label和wasVisited。
復制代碼 代碼如下:
function Vertex(label){
this.label = label;
}
我們將所有頂點保存在數組中,在圖類裡,可以通過他們在數組中的位置引用他們
表示邊
圖的實際信息都保存在“邊”上面,因為他們描述了圖的結構。二叉樹的一個父節點只能有兩個子節點,而圖的結構卻要靈活得多,一個頂點既可以有一條邊,也可以有多條邊和它相連。
我們將表示圖的邊的方法成為鄰接表或者鄰接表數組。它將存儲由頂點的相鄰頂點列表構成的數組
構建圖
定義如下一個Graph類:
復制代碼 代碼如下:
function Graph(v){
this.vertices = v;//vertices至高點
this.edges = 0;
this.adj = [];
for(var i =0;I<this.vertices;++i){
this.adj[i] = [];
this.adj[i].push('');
}
this.addEdge = addEdge;
this.toString = toString;
}
這個類會記錄一個圖表示了多少條邊,並使用一個長度與圖的頂點數來記錄頂點的數量。
復制代碼 代碼如下:
function addEdge(){
this.adj[v].push(w);
this.adj[w].push(v);
this.edges++;
}
這裡我們使用for循環為數組中的每個元素添加一個子數組來存儲所有的相鄰頂點,並將所有元素初始化為空字符串。
圖的遍歷
深度優先遍歷
深度優先遍歷(DepthFirstSearch),也有稱為深度優先搜索,簡稱為DFS。
比如在一個房間內尋找一把鑰匙,無論從哪一間房間開始都可以,將房間內的牆角、床頭櫃、床上、床下、衣櫃、電視櫃等挨個尋找,做到不放過任何一個死角,當所有的抽屜、儲藏櫃中全部都找遍後,接著再尋找下一個房間。
深度優先搜索:
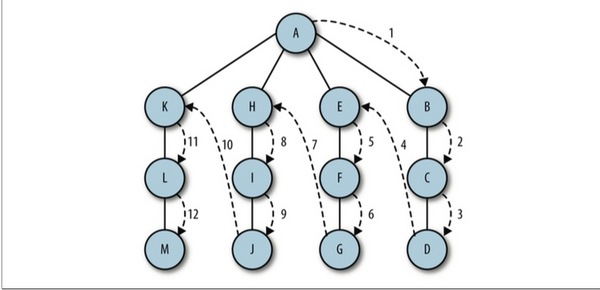
深度優先搜索就是訪問一個沒有訪問過的頂點,將他標記為已訪問,再遞歸地去訪問在初始頂點的鄰接表中其他沒有訪問過的頂點
為Graph類添加一個數組:
復制代碼 代碼如下:
this.marked = [];//保存已訪問過的頂點
for(var i=0;i<this.vertices;++i){
this.marked[i] = false;//初始化為false
}
深度優先搜索函數:
復制代碼 代碼如下:
function dfs(v){
this.marked[v] = true;
//if語句在這裡不是必須的
if(this.adj[v] != undefined){
print("Visited vertex: " + v );
for each(var w in this.adj[v]){
if(!this.marked[w]){
this.dfs(w);
}
}
}
}
廣度優先搜索
廣度優先搜索(BFS)屬於一種盲目搜尋法,目的是系統地展開並檢查圖中的所有節點,以找尋結果。換句話說,它並不考慮結果的可能位置,徹底地搜索整張圖,直到找到結果為止。
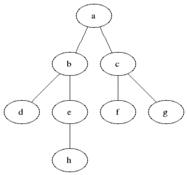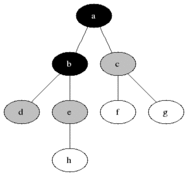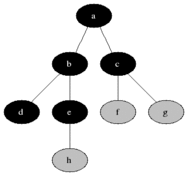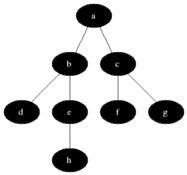
廣度優先搜索從第一個頂點開始,嘗試訪問盡可能靠近它的頂點,如下圖所示:
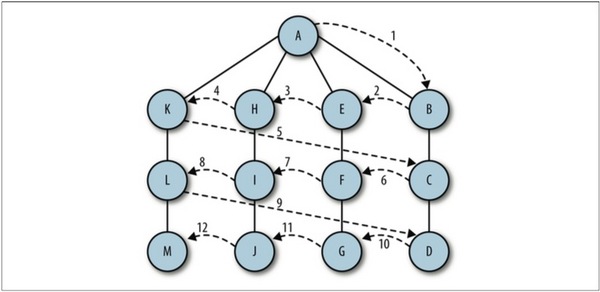
其工作原理為:
1. 首先查找與當前頂點相鄰的未訪問的頂點,將其添加到已訪問頂點列表及隊列中;
2. 然後從圖中取出下一個頂點v,添加到已訪問的頂點列表
3. 最後將所有與v相鄰的未訪問頂點添加到隊列中
下面是廣度優先搜索函數的定義:
復制代碼 代碼如下:
function bfs(s){
var queue = [];
this.marked = true;
queue.push(s);//添加到隊尾
while(queue.length>0){
var v = queue.shift();//從隊首移除
if(v == undefined){
print("Visited vertex: " + v);
}
for each(var w in this.adj[v]){
if(!this.marked[w]){
this.edgeTo[w] = v;
this.marked[w] = true;
queue.push(w);
}
}
}
}
最短路徑
在執行廣度優先搜索時,會自動查找從一個頂點到另一個相連頂點的最短路徑
確定路徑
要查找最短路徑,需要修改廣度優先搜索算法來記錄從一個頂點到另一個頂點的路徑,我們需要一個數組來保存從一個頂點操下一個頂點的所有邊,我們將這個數組命名為edgeTo
復制代碼 代碼如下:
this.edgeTo = [];//將這行添加到Graph類中
//bfs函數
function bfs(s){
var queue = [];
this.marked = true;
queue.push(s);//添加到隊尾
while(queue.length>0){
var v = queue.shift();//從隊首移除
if(v == undefined){
print("Visited vertex: " + v);
}
for each(var w in this.adj[v]){
if(!this.marked[w]){
this.edgeTo[w] = v;
this.marked[w] = true;
queue.push(w);
}
}
}
}
拓撲排序算法
拓撲排序會對有向圖的所有頂點進行排序,使有向邊從前面的頂點指向後面的頂點。
拓撲排序算法與BFS類似,不同的是,拓撲排序算法不會立即輸出已訪問的頂點,而是訪問當前頂點鄰接表中的所有相鄰頂點,直到這個列表窮盡時,才會將當前頂點壓入棧中。
拓撲排序算法被拆分為兩個函數,第一個函數是topSort(),用來設置排序進程並調用一個輔助函數topSortHelper(),然後顯示排序好的頂點列表
拓撲排序算法主要工作是在遞歸函數topSortHelper()中完成的,這個函數會將當前頂點標記為已訪問,然後遞歸訪問當前頂點鄰接表中的每個頂點,標記這些頂點為已訪問。最後,將當前頂點壓入棧中。
復制代碼 代碼如下:
//topSort()函數
function topSort(){
var stack = [];
var visited = [];
for(var i =0;i<this.vertices;i++){
visited[i] = false;
}
for(var i = 0;i<this.vertices;i++){
if(visited[i] == false){
this.topSortHelper(i,visited,stack);
}
}
for(var i = 0;i<stack.length;i++){
if(stack[i] !=undefined && stack[i] != false){
print(this.vertexList[stack[i]]);
}
}
}
//topSortHelper()函數
function topSortHelper(v,visited,stack){
visited[v] = true;
for each(var w in this.adj[v]){
if(!visited[w]){
this.topSortHelper(visited[w],visited,stack);
}
}
stack.push(v);
}