DIV CSS 佈局教程網

我們向搜索引擎提交一個查詢，搜索引擎會從先到後列出大量的結果，這些結果排序的標准是什麼呢？這個看似簡單的問題，卻是信息檢索專家們研究的核心難題之一。

為了說明這個問題，我們來研究一個比搜索引擎更加古老的話題：求醫。比如，如果我牙疼，應該去看怎樣的醫生呢？假設我只有三種選擇：

A醫生，既治眼病，又治胃病；

B醫生，既治牙病，又治胃病，還治眼病；

C醫生，專治牙病。

A醫生肯定不在考慮之列。B醫生和C醫生之間，貌視更應該選擇C醫生，因為他更專注，更適合我的病情。假如再加一個條件：B醫生經驗豐富，有二十年從醫經歷，醫術高明，而C醫生只有五年從醫經驗，這個問題就不那麼容易判斷了，是優先選擇更加專注的C醫生，還是優先選擇醫術更加高明的B醫生，的確成了一個需要仔細權衡的問題。

至少，我們得到了一個結論，擇醫需要考慮兩個條件：醫生的專長與病情的適配程度；醫生的醫術。大家肯定覺得這個結論理所當然，而且可以很自然地聯想到，搜索引擎排序不也是這樣嗎，既要考慮網頁內容與用戶查詢的匹配程度，又要考慮網頁本身的質量。但是，怎麼把這兩種因素結合起來，得到一個，而不是兩個或多個排序標准呢？假如我們把這兩種因素表示成數值，最終的排序依據是把這兩個數值加起來，還是乘起來，或是按決策樹的辦法把它們組織起來？如果是加起來，是簡單相加，還是帶權重加呢？

我們可以根據直覺和經驗，通過試錯的辦法，把這兩個因素結合起來。但更好的辦法是我們能找到一個明確的依據，最好能跟數學這樣堅實的學科聯系起來。說起來，依據樸素的經驗，人類在古代就能建造出高樓；但要建造出高達數百米的 摩天大廈，如果沒有建築力學、材料力學這樣堅實的學科作為後盾，則是非常非常困難的。同理，依據樸素的經驗構建的搜索引擎算法，用來處理上萬的網頁集合應該是沒問題的；但要檢索上億的網頁，則需要更為牢固的理論基礎。

求醫，病人會優先選擇診斷准確、治療效果好的醫生；對於搜索引擎來說，一般按網頁滿足用戶需求的概率從大到小排序。如果用q表示用戶給出了一個特定的查詢，用d表示一個特定的網頁滿足了用戶的需求，那麼排序的依據可以用一個條件概率來表示：

P（d|q）

這個簡單的條件概率，將搜索引擎排序算法與概率論這門堅實的學科聯系了起來，這就像在大海中航行的船只裝備了指南針一樣。利用貝葉斯公式，這個條件概率可以表示為：

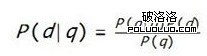
可以清楚地看到，搜索引擎的排序標准，是由三個部分組成的：查詢本身的屬性P（q）；網頁本身的屬性P（d）；兩者的匹配關系P（q|d）。對於同一次查詢來說，所有網頁對應的P（q）都是一樣的，因此排序時可以不考慮，即

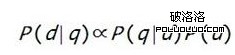
公式左邊，是已知用戶的查詢，求網頁滿足該用戶需求的概率。搜索引擎為了提高響應用戶查詢的性能，需要事先對所有待查詢的網頁做預處理。預處理時，只知道網頁，不知道用戶查詢，因此需要倒過來計算，即分析每個網頁能滿足哪些需求，該網頁分了多大比例來滿足該需求，即得到公式右邊的第一項P（q|d），這相當於上文介紹的醫生的專門程度。比如，一個網頁專門介紹牙病，另一個網頁既介紹牙病又介紹胃病，那麼對於“牙疼”這個查詢來說，前一個網頁的P（q|d）值就會更高一些。

公式右邊的第二項P（d），是一個網頁滿足用戶需求的概率，它反映了網頁本身的好壞，與查詢無關。假如要向一個陌生人推薦網頁（我們並不知道他需要什麼），那麼P（d）就相當於某個特定的網頁被推薦的概率。在傳統的信息檢索模型中，這一個量不太被重視，如傳統的向量空間模型、BM25模型，都試圖只根據查詢與文檔的匹配關系來得到排序的權重。而實際上，這個與查詢無關的量是非常重要的。假如我們用網頁被訪問的頻次來估計它滿足用戶需求的概率，可以看出對於兩個不同的網頁，這個量有著極其巨大的差異：有的網頁每天只被訪問一兩次，而有的網頁每天被訪問成千上萬次。能夠提供如此巨大差異的量，竟長期被傳統的搜索引擎忽略，直到Google發明了pagerank並讓它參與到排序中。Pagerank是對P（d）值的一個不錯的估計，這個因素的加入使搜索引擎的效果立即上升到了一個新的台階。

這個公式同樣回答了上文提出的問題，網頁與查詢的匹配程度，和網頁本身的好壞，這兩個因素應該怎樣結合起來參與排序。這個公式以不可辯駁的理由告訴我們，如果網頁與查詢的匹配程度用P（q|d）來表示，網頁本身的好壞用P（d）來表示，那麼應該按它們的乘積來進行排序。在現代商業搜索引擎中，需要考慮更多更細節的排序因素，這些因素可能有成百上千個，要把它們融合起來是更加復雜和困難的問題。