DIV CSS 佈局教程網

PageRank算法

PageRank算法是谷歌曾經獨步天下的“倚天劍”，該算法由Larry Page和Sergey Brin在斯坦福大學讀研時發明的，論文點擊下載: The PageRank Citation Ranking: Bringing Order to the Web。

本文首先通過一些參考文獻引出問題，然後給出了PageRank的幾種實現算法，最後將其推廣至在MapReduce框架下如何實現PageRank算法。

PageRank的核心思想有2點：

1.如果一個網頁被很多其他網頁鏈接到的話說明這個網頁比較重要，也就是pagerank值會相對較高；

2.如果一個pagerank值很高的網頁鏈接到一個其他的網頁，那麼被鏈接到的網頁的pagerank值會相應地因此而提高。

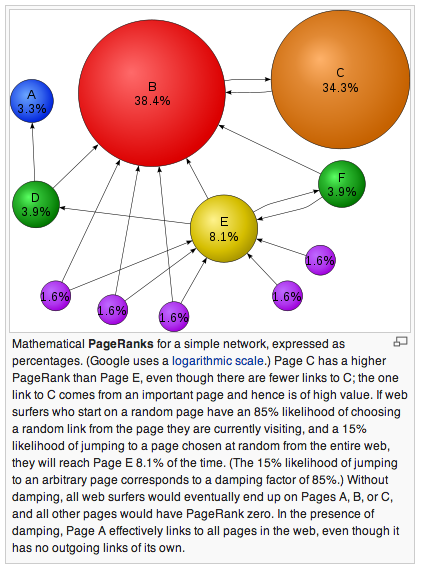
下面是一張來自WikiPedia的圖，每個球代表一個網頁，球的大小反應了網頁的pagerank值的大小。指向網頁B和網頁E的鏈接很多，所以B和E的pagerank值較高，另外，雖然很少有網頁指向C，但是最重要的網頁B指向了C，所以C的pagerank值比E還要大。

參考內容：

1.Wiki about PageRank

2.Google 的秘密- PageRank 徹底解說 中文版

3.數值分析與算法 Page 161 應用實例：Google的PageRank算法

4.Numeric Methods with Matlab 或者中文翻譯版本Matlab數值計算

5.使用 MapReduce 思想計算 PageRank Page 62 PageRank和馬爾可夫鏈

1. 問題背景

來自參考內容3

2.數學建模

來自參考內容3，理解網頁連接矩陣$G$，馬爾科夫過程(“網上沖浪”)，轉移矩陣$A$，概率$p$為用戶點擊當前網頁中的某個鏈接地址的概率(一般都為0.85)。

最後得到一個等式$Ax=x$，這實際上就是求矩陣$A$的特征值為1的特征向量！

下面的內容使用圓盤定理解釋了1是矩陣$A$的主特征值，所以我們可以使用冪法來求解。

關於冪法的詳細介紹參考另一篇文章Numerical Methods Using Matlab: 第三章 矩陣特征值和奇異值求解

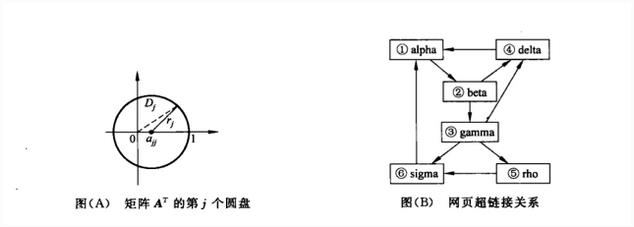
3.求解PageRank

假設有如上圖右側所示的網頁鏈接模型。

(1) 冪法

wiki上有一個PageRank的簡便算法，它不考慮轉移概率，而是采用的是迭代的方式，每次都更新所有網頁的pagerank值，更新的方式就是將每個網頁的pagerank值平攤分給它指向的所有網頁，每個網頁累計所有指向它的網頁平攤給它的值作為它該回合的pagerank值，直到全部網頁的pagerank值收斂了或者滿足一定的阈值條件就停止。

後面的MapReduce框架下PageRank算法的實現就采用了這個思想。考慮轉移概率的情況和這個算法類似，乘上一個轉移概率再加上一個隨機跳轉的概率。

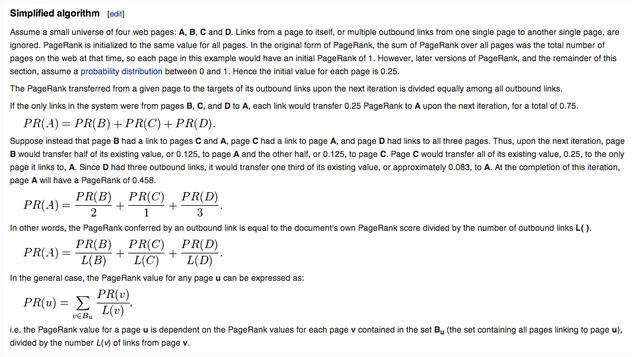
根據上面的思想，下面Matlab代碼實現可以得到各個網頁的PageRank值。

得到的向量$x$保存了各個網頁的pagerank值，雖然鏈接數目一樣，但是網頁①比網頁④和網頁⑤都高，而網頁②的pagerank值第二高，因為網頁①鏈接到了它上面，相當於沾了網頁①的光。

這篇文章給出該算法的一個Python版本實現，該博主使用第三方模塊python-graph，python-graph模塊實現了很多圖算法，該模塊的使用示例，使用前需要先安裝，代碼如下：

Python版本的算法實現：

經過32次迭代之後得到的結果如下，和前面的結果一致：

(2) 利用馬爾可夫矩陣的特殊結構

來自參考內容4，其中$delta=frac{1-p}{n}$

也就是將矩陣$A$進行分解，並不需要顯示求出矩陣$A$，然後便是求解一個線性方程組即可。

(3) 巧妙解法：逆迭代算法

巧妙利用Matlab中的精度誤差導致原本是一個奇異矩陣的$I-A$變成一個非奇異矩陣，運行時只是會有些警告提示，但是運行結果和其他算法一樣。

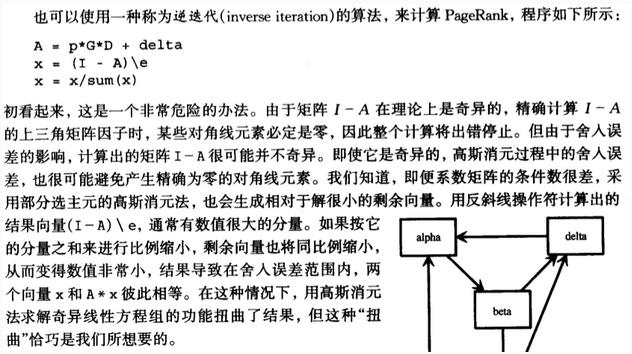
最後，附上參考內容4中給出的一份好代碼，用於模擬隨機沖浪生成矩陣$G$的代碼

4.MapReduce框架下PageRank算法的實現

利用前面wiki上的迭代(或者冪法)的思想來實現MapReduce框架下PageRank算法很簡單，可以先閱讀下參考內容5。

這篇文章using-mapreduce-to-compute-pagerank更加詳細，可以參考

以下是我的大數據的一次作業，要求是參考wiki上的簡便算法，實現MapReduce框架下的PageRank算法。給的數據集是Twitter的用戶之間的關系，可以看做是網頁之間的關系，但是助教沒要求寫代碼以及運行這個數據集(有1G多)，所以下面只是一個Python版本的理想可行版本，並沒有通過實際大數據集的驗證，另外，博主暫時還不太會Python的mapreduce框架中的一些函數，所以實現的是一個簡明的可以測試的PageRank算法。

1.輸入輸出格式

map函數的輸入是<節點，從該節點引出的邊列表>，其中節點是一個類，包含了其當前的pagerank值，輸出是<節點，反向節點pagerank值/反向節點引出邊的總數>；

reduce函數的輸入是<節點，反向節點pagerank值/反向節點引出邊的總數>，輸出是<節點，從該節點引出的邊列表>，其中節點包含了其更新後的pagerank值。

偽代碼： [一時犯二寫了個英文形式的 ]

2.示例演示

假設用戶1，2，3，4是如下圖所示的關系：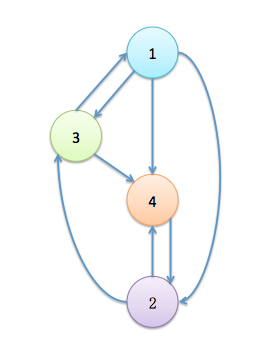

假設有2個mapper(A和B)和1個reducer(C)，初始時4個節點的pagerank值都是0.25

其中，關於用戶1和2的數據被mapperA讀取並處理，關於用戶3和4的數據被mapperB讀取並處理 [經驗證，即使一個用戶的數據是由不同的mapper來讀取的，最終收斂到的結果差不多]

map的輸入輸出結果如下：

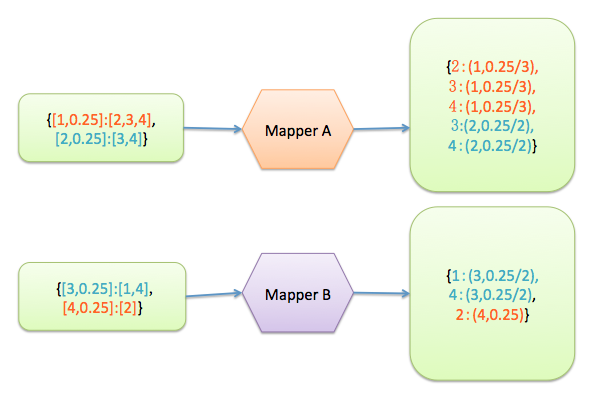
reduce的輸入輸出結果如下，輸入是2個mapper的輸出，輸出的結果中更新了節點的pagerank值

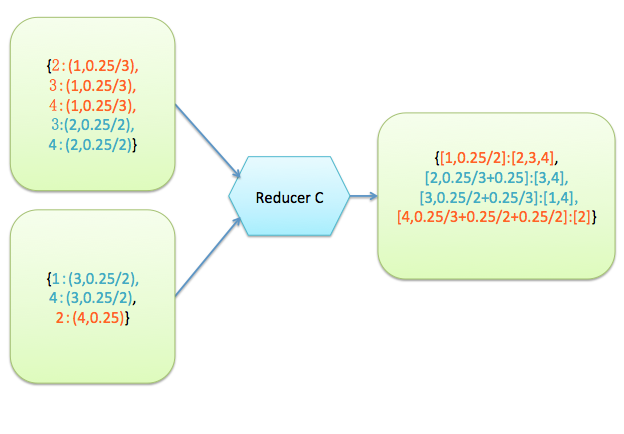
reducer處理完了之後又將它的結果輸入給mapper處理，直到迭代的次數超過了設定值或者兩次迭代之後得到的所有節點的pagerank值之差的總和(也可以是取二范數)小於設定的阈值。

3.示例的實驗結果

(1)首先是使用Matlab采用冪法的方式計算出在p=1.0的情況下示例得到的結果 [它的主要作用是驗證後面python版本的正確性]

matlab源碼如下：

結果為：

(2)matlab版本的page rank沒有采用mapreduce的思想進行迭代，所以我另外寫了一個python版本的利用mapreduce思想實現的pagerank算法(注：我並沒有使用python的map和reduce函數去實現，而是使用更加容易明白的實現)，使用的阈值為0.0001，最多迭代的次數為100次。

得到的結果為如下，總共迭代了15次

上面的結果和Matlab用冪法得到的pagerank值差別很小，可以認為是正確的，所以說明了使用這種mapreduce輸入輸出格式的正確性。

OK，差不多了，希望對需要理解PageRank算法的人有幫助！